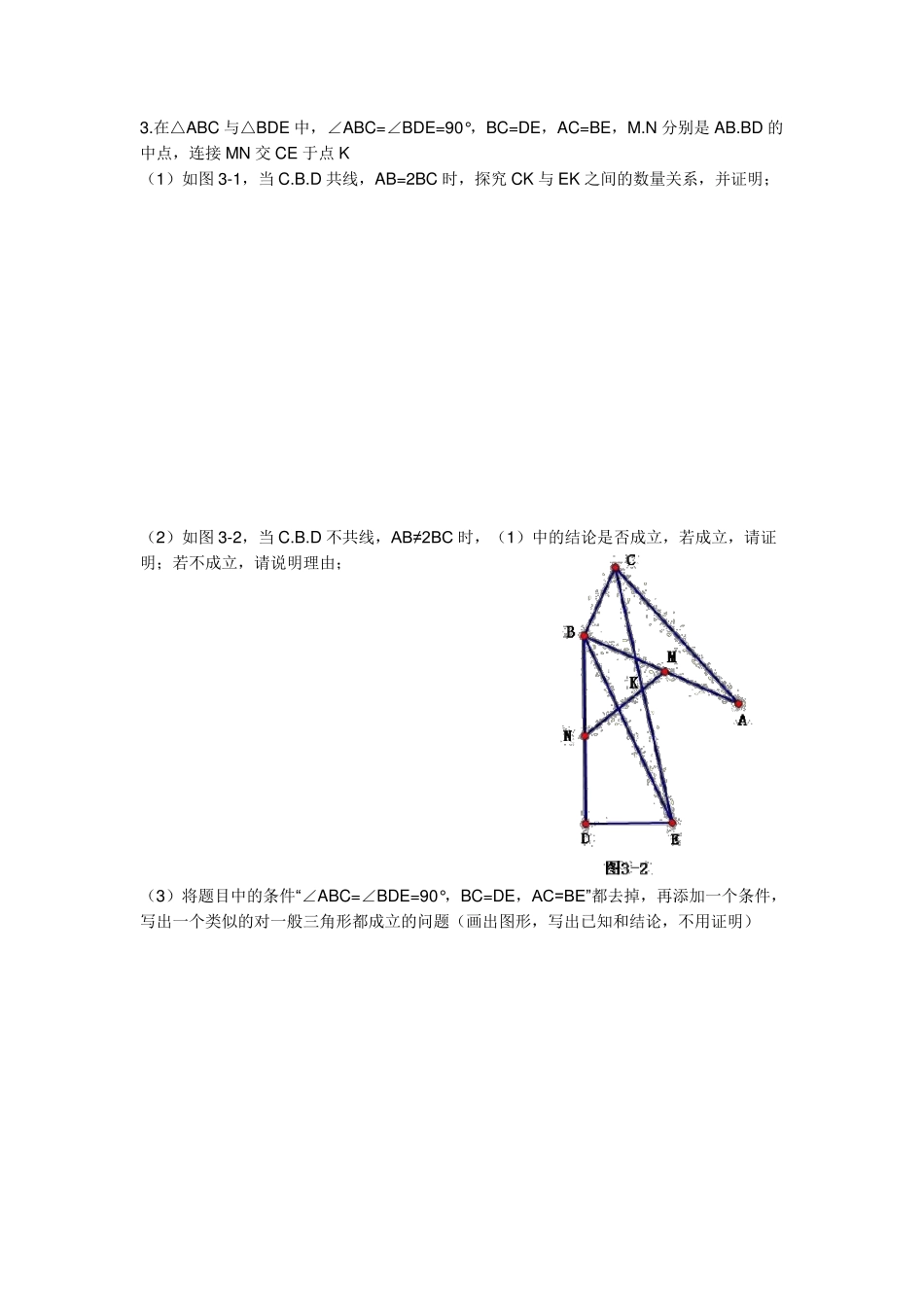
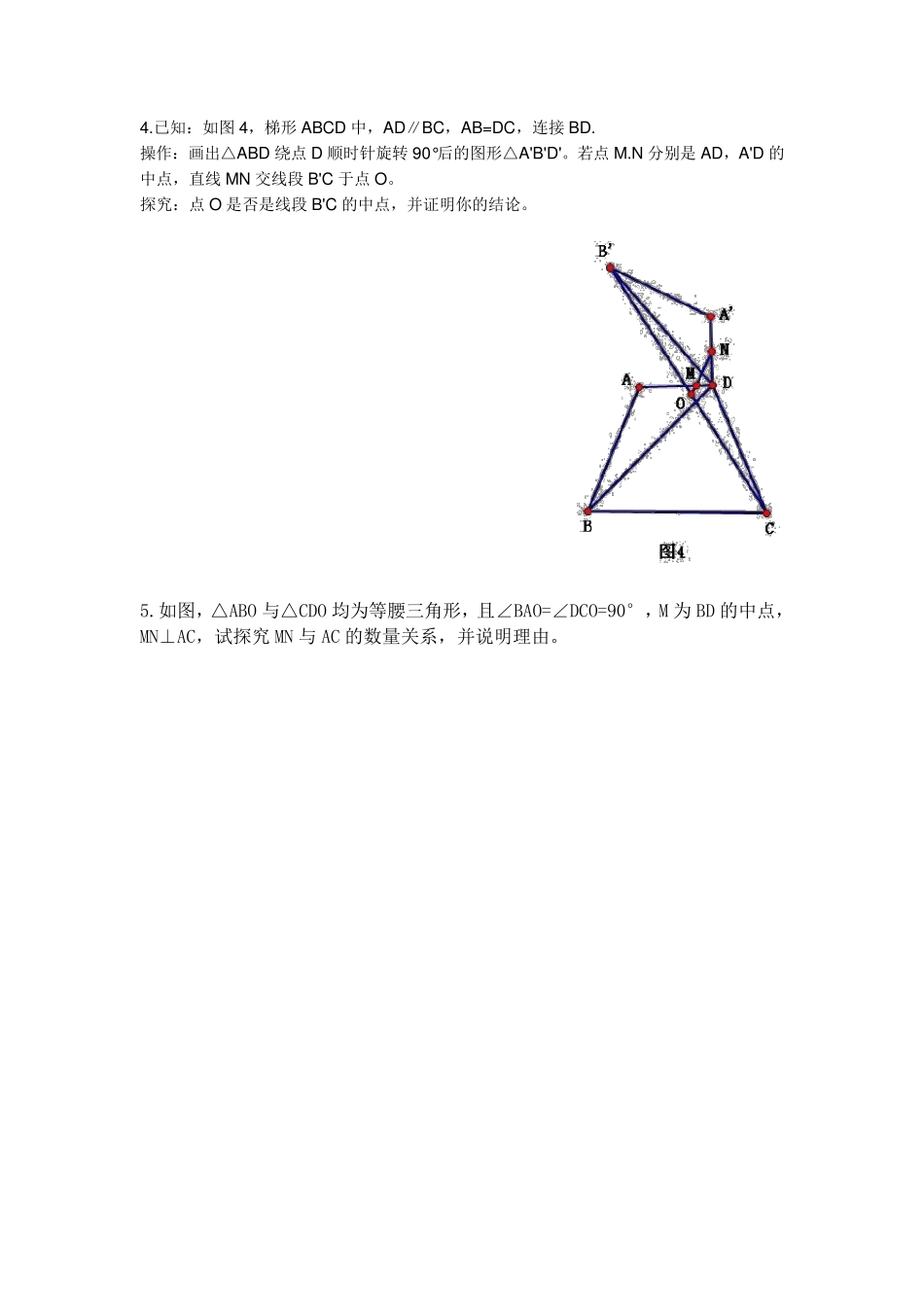
初二几何试题 1.如图1,已知△ABC,∠ACB=90°,分别以AB、BC为边向外作△ABD与△BCE,且DA=DB,BE=EC,若∠ADB=∠BEC=2∠ABC,连接 DE 交 AB 于点 F,试探究线段 DF 与 EF 的 数量关系,并加以证明。 2.如图2-1,在 Rt△ABC 中,∠ACB=90°,∠BAC=60°, (1)将 Rt△ABC 绕点 A 逆时针旋转 90°,得到 Rt△AC'B',直线 BB'交直线 CC'于点 D,连接 AD.探究:AD 与 BB'之间的 关系,并说明理由。 (2)如图2-2,若将 Rt△ABC 绕点 A 逆时针旋转任意角度,其他条件不变,还有(1)的结论吗?为什么? 3.在△ABC 与△BDE 中,∠ABC=∠BDE=90°,BC=DE,AC=BE,M.N 分别是 AB.BD 的中点,连接 MN 交 CE 于点 K (1)如图 3-1,当 C.B.D 共线,AB=2BC 时,探究 CK 与EK 之间的数量关系,并证明; (2)如图 3-2,当 C.B.D 不共线,AB≠2BC 时,(1)中的结论是否成立,若成立,请证明;若不成立,请说明理由; (3)将题目中的条件“∠ABC=∠BDE=90°,BC=DE,AC=BE”都去掉,再添加一个条件,写出一个类似的对一般三角形都成立的问题(画出图形,写出已知和结论,不用证明) 4.已知:如图4,梯形ABCD 中,AD∥BC,AB=DC,连接BD. 操作:画出△ABD 绕点D 顺时针旋转90°后的图形△A'B'D'。若点M.N 分别是AD,A'D 的中点,直线MN 交线段B'C 于点O。 探究:点O 是否是线段B'C 的中点,并证明你的结论。 5.如图,△ABO 与△CDO 均为等腰三角形,且∠BAO=∠DCO=90°,M 为BD 的中点, MN⊥AC,试探究MN 与AC 的数量关系,并说明理由。 MM1、如图,已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC,延长BE交AC 于F,求证:AF=EF.(10 分) (提示:延长AD 到M 使M D=AD,连接BM ) 2、如图,△ABC 中,D 是BC 的中点,DE⊥DF,试判断 BE+CF 与 EF 的大小关系,并证明你的结论.(10 分) (提示:延长ED 到M 使M D=M D,连接CM 、FM ) 3、如图,在△ABC 中,∠ABC=60°,AD、CE 分别平分∠BAC、∠ACB,求证:AC=AF+CD. (10 分) 4、 如图甲,点 C 为线段 AB 上一点,△ACM、△CBN是等边三角形,直线 AN、MC 交于点 E,直线 BM、CN交于点 F.(10 分) (1)求证:AN=BM; (2)求证:△CEF 是等边三角形; 5、如图,在△ABC 内,∠BAC=60°,∠ACB=40°,P、Q 分别在BC、CA 上,并且 AP、BQ 分别为∠BAC、...