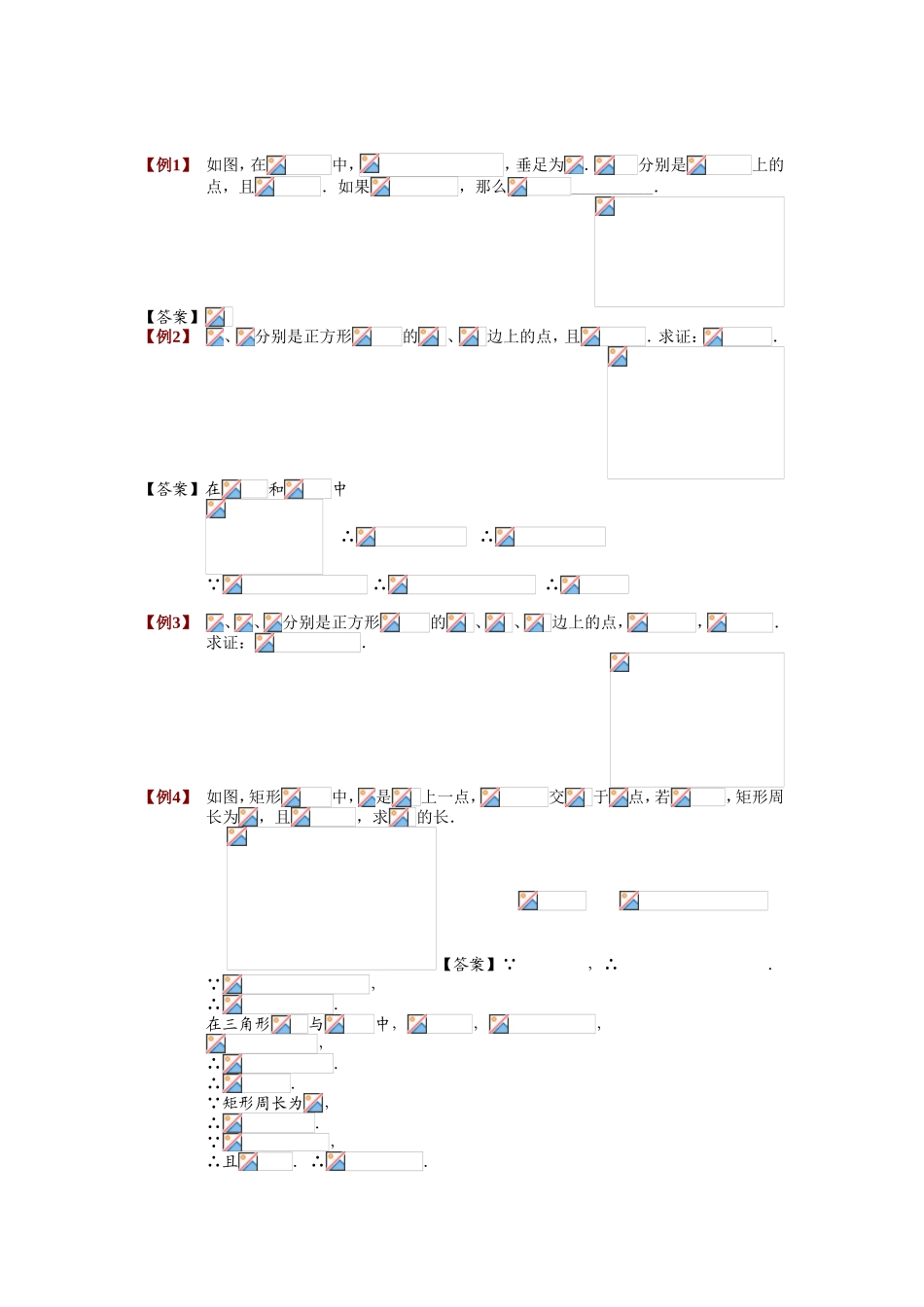
【例1】如图,在中,,垂足为.分别是上的点,且.如果,那么__________.【答案】【例2】、分别是正方形的、边上的点,且.求证:.【答案】在和中∴∴ ∴∴【例3】、、分别是正方形的、、边上的点,,.求证:.【例4】如图,矩形中,是上一点,交于点,若,矩形周长为,且,求的长.【答案】 ,∴. ,∴.在三角形与中,,,,∴.∴. 矩形周长为,∴. ,∴且.∴.即【例5】如图,已知中,,三角形的顶点在相互平行的三条直线上,且之间的距离为,之间的距离为,则的长是______.CBAl3l2l1【答案】【例6】两个全等的、的三角板、,如右下图所示摆放,、、在一条直线上,连结.取的中点,连结、,试判断的形状,并说明理由.【解析】判断是等腰直角三角形.理由:如图,连结. ,,∴ ,∴又 是的中点,∴∴∴∴∴ ,∴∴,而,∴即,∴是等腰直角三角形.【例7】已知等腰直角三角形,为直角,为的中点..求证:.求证:.【例8】如图所示,已知在等腰直角三角形中,是直角,是上一点,,的延长线交于,若,求证:是的中点.【答案】过作垂直于交延长线于点;易证,;进而证明,得到,则为中点.【例9】如图所示,在等边中,,为的中心,为的中点,求证.【答案】如图所示,延长至点,使,连接、、、、.因为,,,故≌,则,.因为,则,.因为为的中心,则,.因为,故≌,从而.因为,故.【点评】如果具备三角形相似的知识,我们就可以采取下面的解法.如图所示,取的中点,连接、、、.因为为的中心,故,.因为,,故.因为,,故,因为,故∽,,则、、、四点共圆.因为,故.【例10】已知为等腰直角的斜边上任意一点,、分别为、之垂线,垂足为、.为之中点.则、、组成等腰直角三角形.【答案】解法一:如图,连接,则为之中线,亦为之高.∴. ,∴为矩形,故.又 ,∴为等腰直角三角形,∴.∴.又 ,,∴,∴,. ,∴,即.∴为等腰直角三角形.解法二:如图,由作,,则显然由于为之中点,,,∴为正方形,故.又设交于,则 ,,∴.而.∴为矩形,故.同理.又 ,∴.∴为等腰直角三角形,∴,故.又,.∴,∴,.又,∴.即,故为等腰直角三角形.解法三:如图,延长到,使,连接. ,∴、、、点组成平行四边形.∴,.又 ,∴,∴.又 ,,∴.同理. 为矩形,∴,,故.而,∴,.∴.∴,,. ,∴.故.∴为等腰直角三角形.而为底边之中点,所以亦为等腰直角三角形.解法四:如图,连接,则因为为之中点,所以,平分,即.由向引垂线,向引垂线,显然为矩形.则.又 为等腰直角三角形,.又 ,,,∴为矩形,故.于是在和中,,,,∴,∴,故.又 , ,即.同理,为等腰直角三角形.解法五:如图,连接、. ,为等腰直角三角形,∴.∴、、、点共圆.∴.又 ,∴,∴、、、点共圆.∴,,∴是等腰直角三角形.【例11】长方形中,,,的角平分线交于点,交于,则_________.【解析】由,平分可知.由基本图可知,故又,,故.由勾股定理可知,.从而可知.【答案】5【例12】如图,设和都是正三角形,且,则的度数是()A.B.C.D.【答案】分析既然题目这样问,说明这两个角之间必然能找到一定的联系.解易知,,于是,从而,在考虑到,有:从而,选B。【例13】已知:是的高,点在的延长线上,,点在上,,求证:⑴;⑵.【答案】如图,设交于.⑴由,,知.而,故.由已知,有,,从而,即有.⑵由⑴可得,而..从而可得,即.【例14】如图,的边在直线上,,且;的边也在直线上,边与边重合,且.⑴在图1中,请你通过观察、测量,猜想并写出与所满足的数量关系和位置关系;⑵将沿直线向左平移到图2的位置时,交于点,连结,.猜想并写出与所满足的数量关系和位置关系,请证明你的猜想;⑶将沿直线向左平移到图3的位置时,的延长线交的延长线于点,连结,.你认为⑵中所猜想的与的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.图⑴lPC(F)BA(E)图⑵Q←lPFECBA图⑶←QAEBCFPl4321ABCEFPlQ【答案】(1);.(2);.①由已知,得,∴.又 ,∴.∴.在和中,,∴,∴.②如图,延长交于点. ,∴....