正态分布的概念概述VIP免费

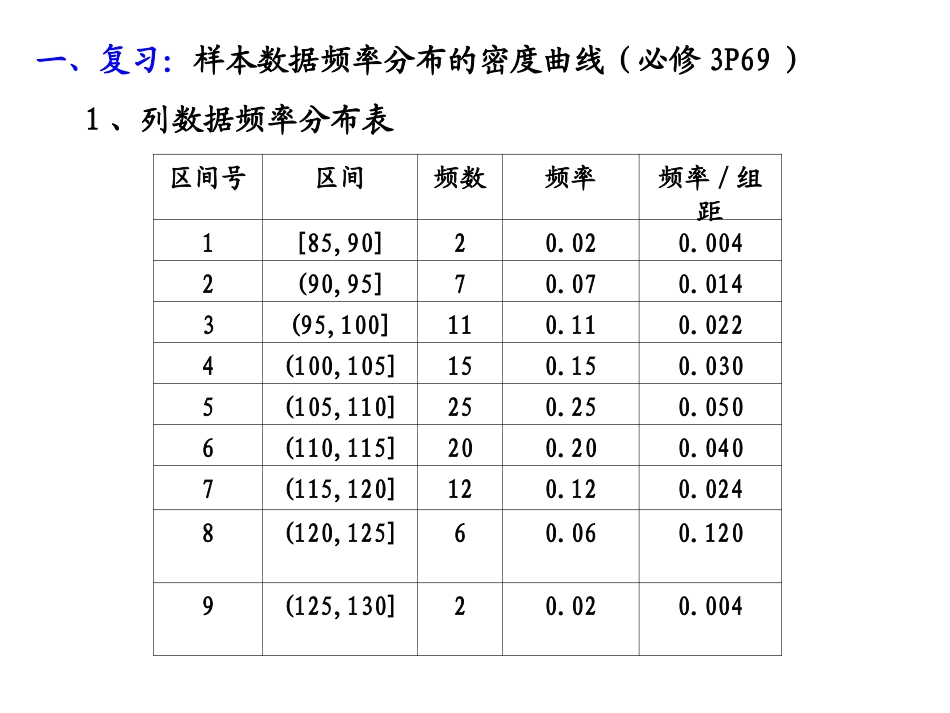
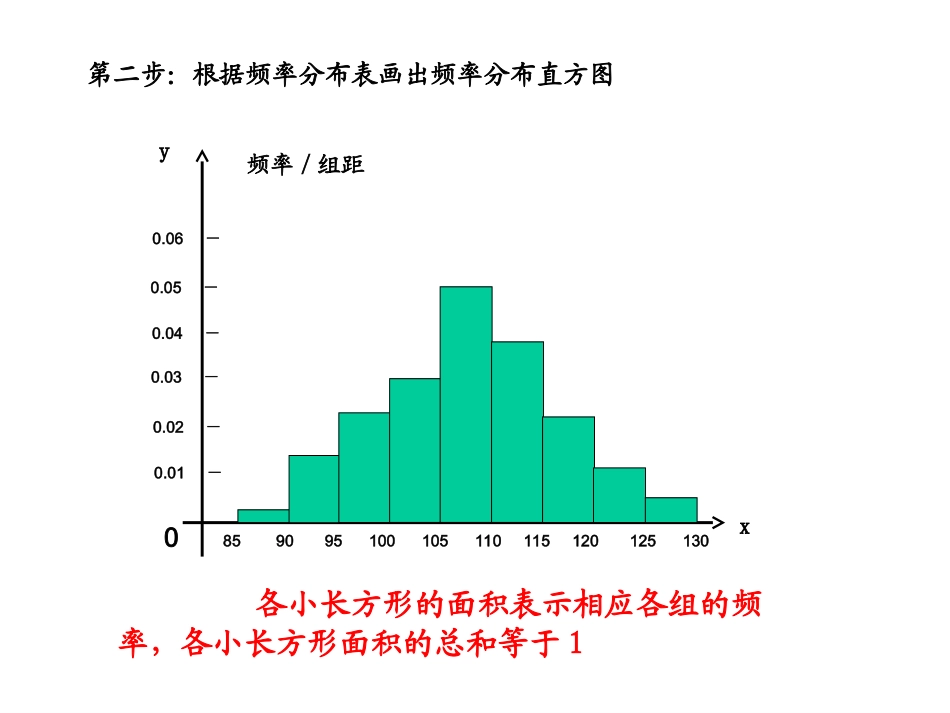
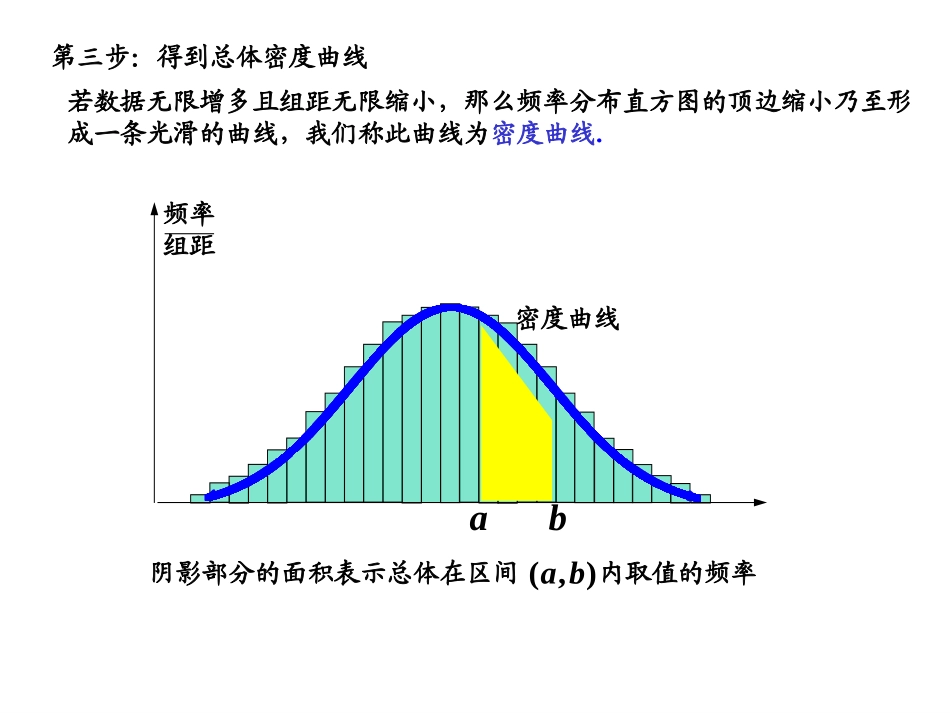
区间号区间频数频率频率/组距1[85,90]20.020.0042(90,95]70.070.0143(95,100]110.110.0224(100,105]150.150.0305(105,110]250.250.0506(110,115]200.200.0407(115,120]120.120.0248(120,125]60.060.1209(125,130]20.020.004一、复习：样本数据频率分布的密度曲线（必修3P69）1、列数据频率分布表第二步：根据频率分布表画出频率分布直方图xy频率/组距08590951001051101151201251300.01－0.02－0.03－0.04－0.05－0.06－各小长方形的面积表示相应各组的频率，各小长方形面积的总和等于1ab频率组距第三步：得到总体密度曲线若数据无限增多且组距无限缩小，那么频率分布直方图的顶边缩小乃至形成一条光滑的曲线，我们称此曲线为密度曲线．密度曲线),(ba阴影部分的面积表示总体在区间内取值的频率二、正态分布（1）正态函数的定义（总体标准差是衡量总体波动大小的特征数，常用样本标准差去估计）22()21(),(,)2xfxex2==ED其中：，（2）正态分布与正态曲线若总体密度曲线就是或近似地是函数,,21222xexfx的图象，则其分布叫正态分布，记作：xf的图象称为正态曲线。2(,)NRxexfx,2122相应的函数表达式是：当时，正态总体称为标准正态总体，记为1,0(0,1)NRxexfx,221)(28)1(2）（Rxexfx,22)(32)1(2）（101，）（212，）（221(1)()2xfxe1(3)1,21.已知函数表达式，试指出相应的参数：(3)正态曲线的性质：①曲线在X轴的上方，与X轴不相交；②曲线关于对称，且在时位于最高点；xxx③当时曲线上升；当时曲线下降；左右可以无限延展，以X轴为渐近线，向它无限靠近。x④曲线与X轴之间的面积为1；⑤曲线的形状由确定：越小，曲线越“瘦高”，表示总体越集中；越大，曲线越“矮胖”，表示总体越分散；2.画出三条正态曲线：;5.0,1)1(;1,0)2(;2,1)3((4).概率(P73):若，则对于任何实数a>0,2(,)xN,()aaPaxadxaa表示图中阴影部分的面积()0.6826Px(22)0.9544Px(33)0.9974Px要记住：正态总体在以外取值的概率只有4.6％，在以外取值的概率只有0.3％。2,23,33、标准正态总体的函数为（1）证明f(x)是偶函数；（2）求f(x)的最大值；（3）利用指数函数的性质说明f(x)的增减性。221(),(,).2xfxex4、若一个正态分布的概率函数是一个偶函数且该函数的最大值等于，求该正态分布的概率密度函数的解析式。1422321()42xfxe2025301510xy535125、如图，是一个正态曲线，根据图象（1）写出其正态分布的概率密度函数的解析式；（2）求出总体随机变量的期望和方差；（3）求概率2(20)41(1)()2xfxe(202202)Px(2)()20,()2ExDx(3)0.6826思考：(20202)?Px