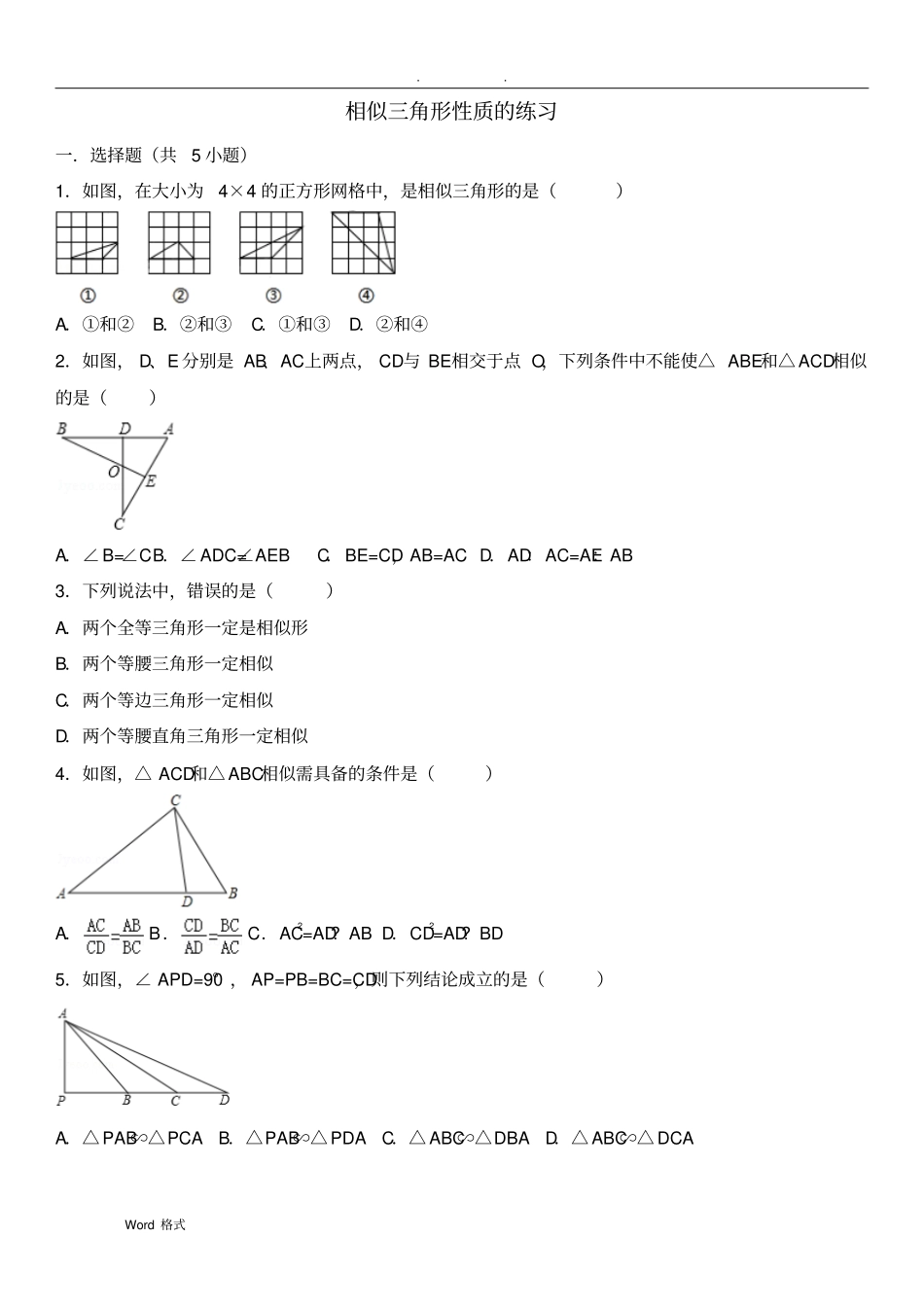
. . Word 格式相似三角形性质的练习一.选择题(共5 小题)1.如图,在大小为4×4 的正方形网格中,是相似三角形的是()A.①和②B.②和③C.①和③D.②和④2.如图, D、E 分别是 AB、AC上两点, CD与 BE相交于点 O,下列条件中不能使△ ABE和△ ACD相似的是()A.∠ B=∠C B.∠ ADC=∠AEB C.BE=CD,AB=AC D.AD:AC=AE:AB3.下列说法中,错误的是()A.两个全等三角形一定是相似形B.两个等腰三角形一定相似C.两个等边三角形一定相似D.两个等腰直角三角形一定相似4.如图,△ ACD和△ ABC相似需具备的条件是()A. B. C.AC2=AD? AB D.CD2=AD? BD5.如图,∠ APD=90° , AP=PB=BC=CD,则下列结论成立的是()A.△ PAB∽△PCA B.△PAB∽△ PDA C.△ ABC∽△DBA D.△ ABC∽△ DCA . . Word 格式二.填空题(共3 小题)6.如图,在△ ABC中,∠ C=90° , BC=16cm,AC=12cm,点 P 从点 B 出发,沿 BC以 2cm/s 的速度向点C移动,点 Q从点 C出发,以 1cm/s 的速度向点 A移动,若点 P、Q分别从点 B、C同时出发,设运动时间为 t s ,当 t= 时,△ CPQ与△CBA相似.7.如图,已知直线y=﹣x+2 与 x 轴交于点 A,与 y 轴交于点 B,在 x 轴上有一点 C,使 B、O、C三点构成的三角形与△ AOB相似,则点 C的坐标为.8.如图,矩形 ABCD中, AD=2,AB=5,P为 CD边上的动点,当△ ADP与△BCP相似时, DP= .三.解答题(共2 小题)9.如图,已知:∠ BAC=∠EAD,AB=20.4,AC=48,AE=17,AD=40.求证:△ ABC∽△AED.10.如图示,正方形ABCD的顶点 A 在等腰直角三角形DEF的斜边 EF上,EF与 BC相交于点 G,连接 CF.①求证:△ DAE≌△ DCF;②求证:△ ABG∽△ CFG.. . Word 格式. . Word 格式相似三角形性质的练习参考答案与试题解析一.选择题(共5 小题)1.如图,在大小为4×4 的正方形网格中,是相似三角形的是()A.①和②B.②和③C.①和③D.②和④【解答】 解:①和③相似, 由勾股定理求出①的三角形的各边长分别为2、、;由勾股定理求出③的各边长分别为2、2、2,∴=,=,即==,∴两三角形的三边对应边成比例,∴①③相似.故选 C.2.如图, D、E 分别是 AB、AC上两点, CD与 BE相交于点 O,下列条件中不能使△ ABE和△ ACD相似的是()A.∠ B=∠C B.∠ ADC=∠AEB C.BE=CD,AB=AC D.AD:AC=AE...