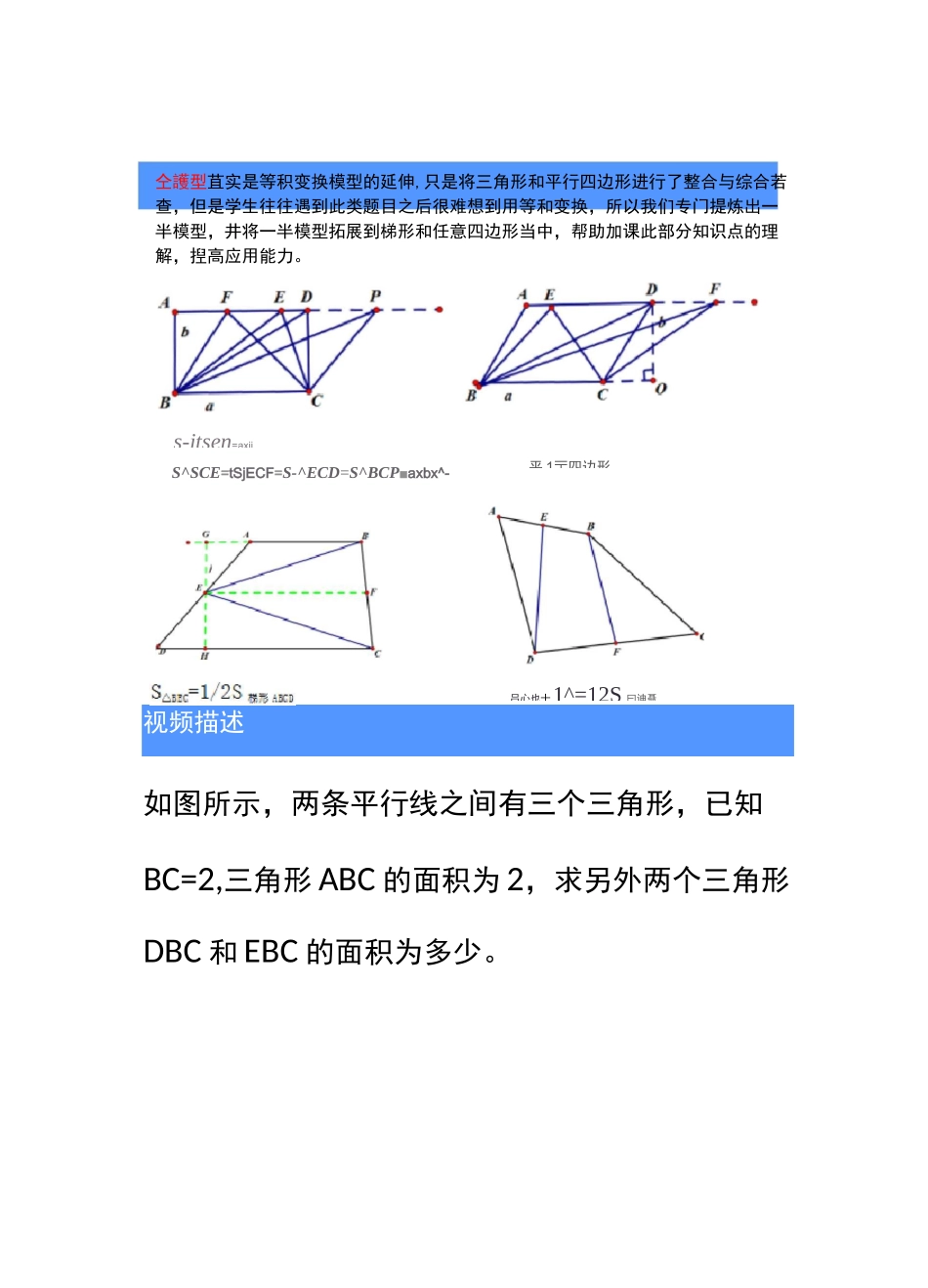
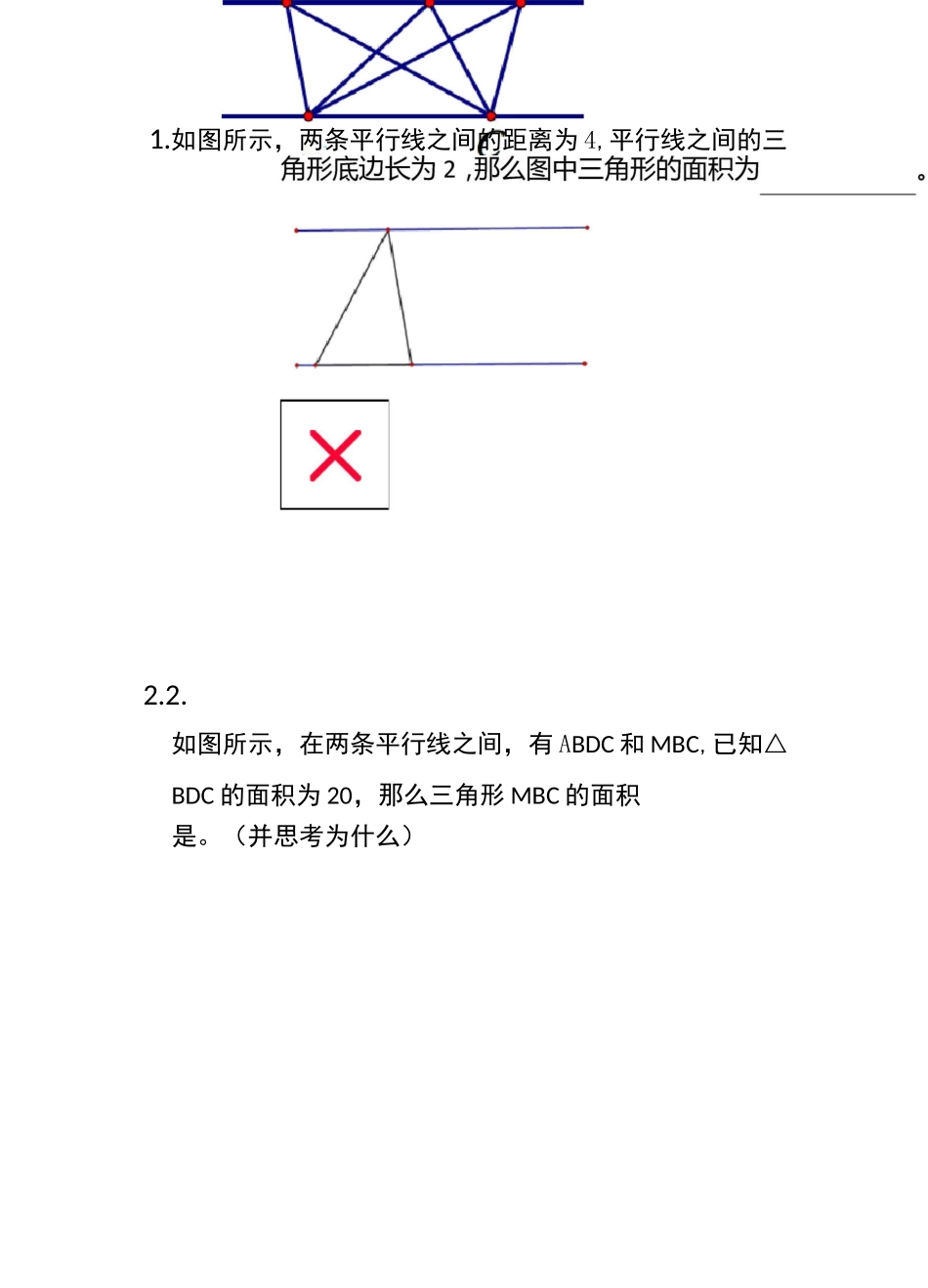
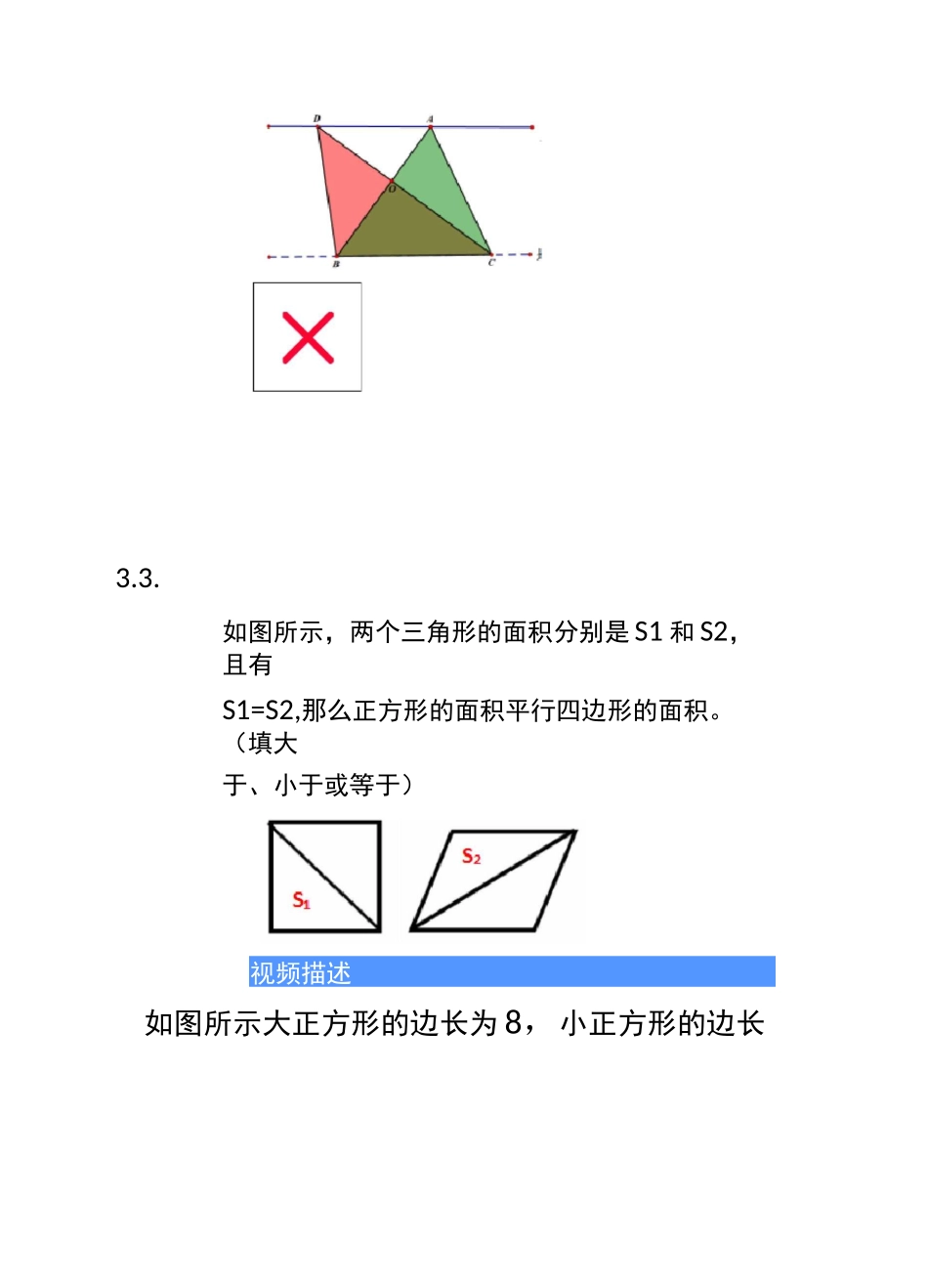
仝護型苴实是等积变换模型的延伸,只是将三角形和平行四边形进行了整合与综合若查，但是学生往往遇到此类题目之后很难想到用等和变换，所以我们专门提炼出一半模型，井将一半模型拓展到梯形和任意四边形当中，帮助加课此部分知识点的理解，揑高应用能力
视频描述如图所示，两条平行线之间有三个三角形，已知BC=2,三角形 ABC 的面积为 2，求另外两个三角形DBC 和 EBC 的面积为多少
s-jtsen=axij平 1〒四边形S^SCE=tSjECF=S-^ECD=S^BCP■axbx^-吕心也十1^=12S 曰迪聂1
如图所示，两条平行线之间的距离为 4,平行线之间的三2
如图所示，在两条平行线之间，有 ABDC 和 MBC,已知△BDC 的面积为 20，那么三角形 MBC 的面积是
（并思考为什么）3
如图所示，两个三角形的面积分别是 S1 和 S2，且有S1=S2,那么正方形的面积平行四边形的面积
（填大于、小于或等于）视频描述如图所示大正方形的边长为 8，小正方形的边长为 4，那么图中阴影部分的面积为
已知正方形 ABCD 的边长为 10 正方形 BEFG 的边长为 6,正方形 JCIH 面积未知，求阴影部分面积=
DHE视频描如图所示，矩形 ABCD 的长为 8,宽为 5,那么阴影部分的面积为多少
角形的面积为CC1
如图所示已知平行四边形的面积为 10，那么两个阴影三2
如图所示，已知两个阴影三角形面积之和为 12，求平行四边形的面积为
已知平行四边形的面积为 28，求所有阴影三角形的面积之和为
已知梯形的 ABCD 的面积为 20,E 点为 AD 边的中点，那么三角形 BEC 的面积的面积为多少E 点是边 BC 上的中点，梯形的面积为 38，那么阴影部分三角形的面积为
如图所示，梯形 ABCD，已知 F 点是 BC 边的中点，S^AB
