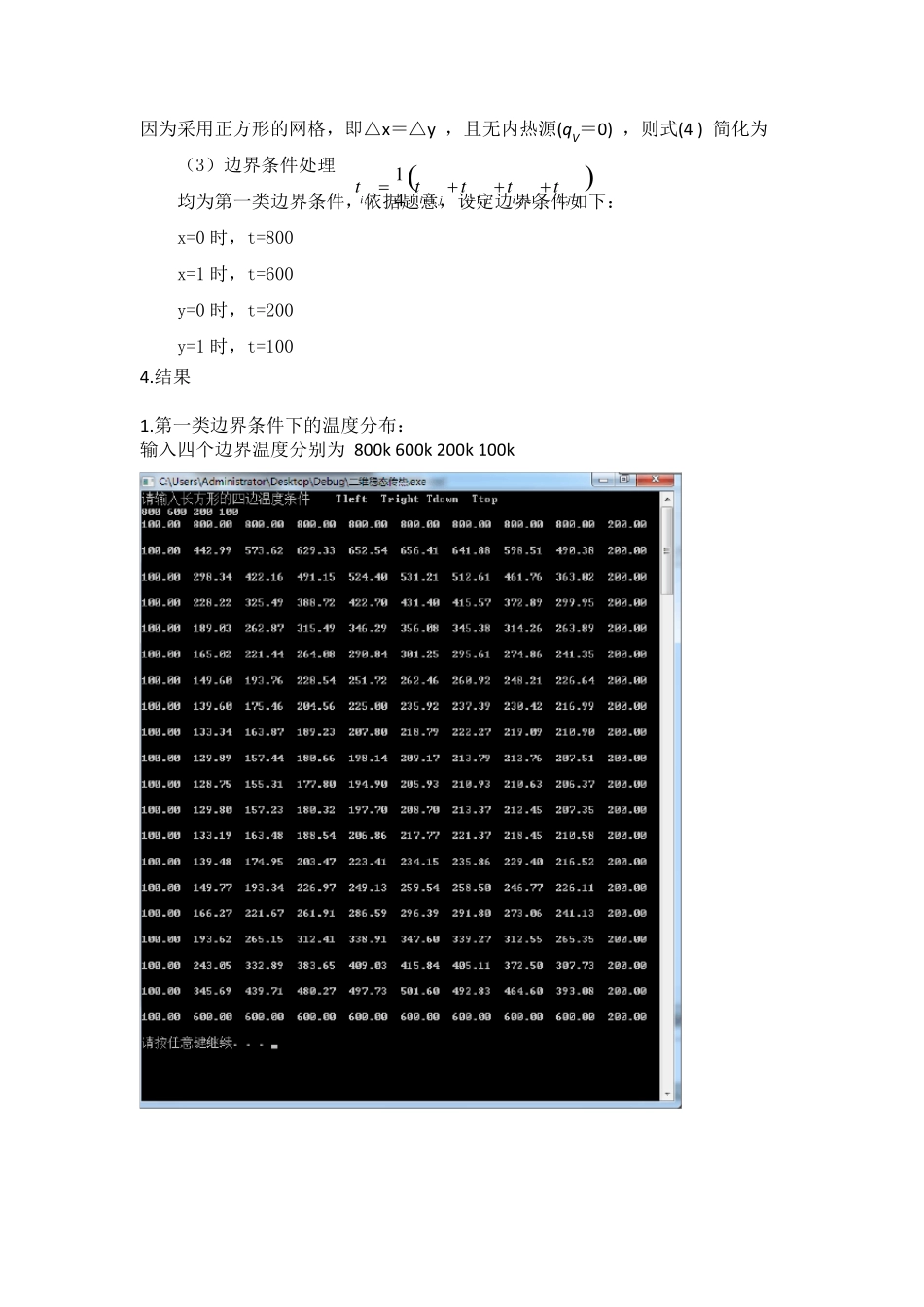
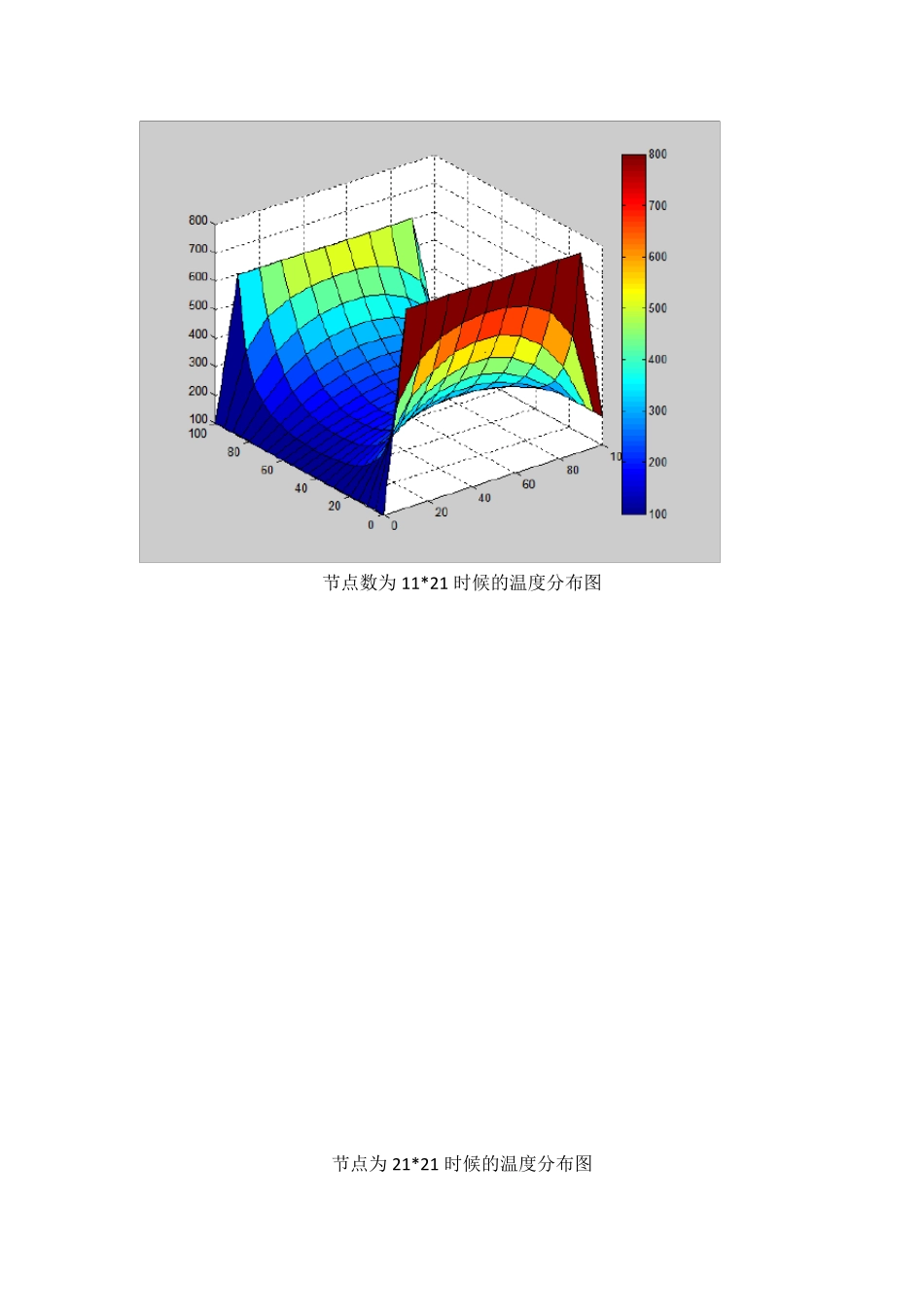
问题:假定一个方形材料100mm*100mm,四边分别为第一、第二、第三类边界条件,无内热源,导热系数为常数,分析该区域内的温度变化。 2.求解过程—热平衡法 (1)区域离散化 对正方形区域进行离散,将该区域划分成不同节点数的不重叠子区域。设置节点时采用内点法。 (2)控制方程离散化 依据题意,二维稳态无源项的纯导热问题的控制方程如式(1) 22220TxTy .…...……………….(1) 扩散项——中心差分,如式(2)(3) ……………………….(2) ……………………….(3) 将(2)、(3)、(4)式代入方程(1)可得到离散后的代数方程(5) 1 ,,1 ,,1,,122220()()iji jiji ji ji jttttttxy…..…….(4) 21 ,,1 ,222,2()()iji jiji jtttd tOxdxx2,1,,1222,2()()i ji ji ji jtttd tOydyy因为采用正方形的网格,即△x=△y ,且无内热源(qV=0) ,则式(4 ) 简化为 (3)边界条件处理 均为第一类边界条件,依据题意,设定边界条件如下: x=0 时,t=800 x=1 时,t=600 y=0 时,t=200 y=1 时,t=100 4.结果 1.第一类边界条件下的温度分布: 输入四个边界温度分别为 800k 600k 200k 100k ,1 ,1 ,,1,114i jijiji ji jttttt 节点数为 11*21 时候的温度分布图 节点为 21*21 时候的温度分布图 2,边界为第二类边界时的结果 边界条件: X=0,t=10y Y=0,t=10x X=100,t=10y+10(M-1) Y=100,t=10x+10(N-1) 结果: 3,边界为第一、第二类边界时: X=0,t=10y Y=0,t=10x X=100,t=100 Y=100,t=200 3.程序 //二维稳态导热数值计算程序 //作者:石明 //日期:2012 年12 月25 日 //功能:得出四边第一类边界条件下的长方形的温度分布 #inclu de #inclu de #inclu de #define M 10 #define N 20 void main() { /****************键盘输入边界条件**************/ float Tleft, Tright, Tdown, Ttop; printf("请输入长方形的四边温度条件 Tleft Tright Tdown Ttop\n"); scanf("%f%f%f%f",&Tleft,&Tright,&Tdown,&Ttop); /****************二维计算区域离散**************/ float T[M][N]; float Tcopy[M][N]; // 定义迭代对比矩阵 int i,j,k; /*****************边界条件设...