梁的弯曲应力VIP免费

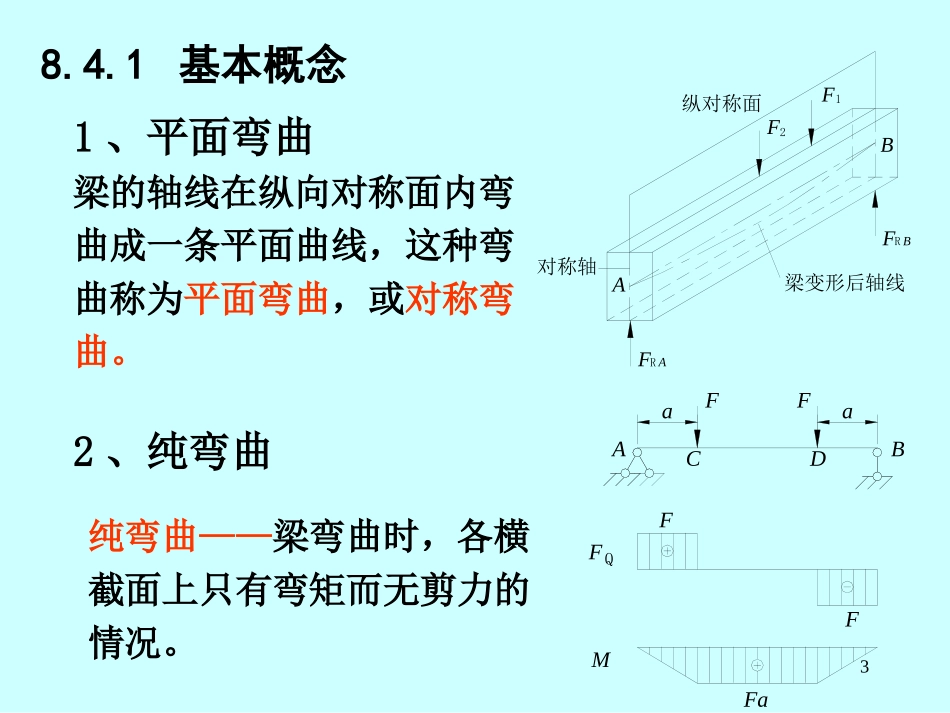
18.1.2应力的概念正应力：与截面垂直的应力分量切应力：与截面相切的应力分量应力：内力在一点处的分布集度单位：帕斯卡，符号Pa，常用千帕（kPa）、兆帕（MPa）及吉帕（GPa），1Pa=1N/m2平均应力pm=F/A应力pτσ△FM△A0dlimdAFFpAA28.4.1基本概念8.4平面弯曲杆件的应力和变形8.4.2梁横截面上的正应力公式8.4.3梁的切应力8.4.4梁的挠度和转角38.4.1基本概念1、平面弯曲FAFF12纵对称面AB对称轴梁变形后轴线RRFB梁的轴线在纵向对称面内弯曲成一条平面曲线，这种弯曲称为平面弯曲，或对称弯曲。2、纯弯曲ABCDaaFMFFFaFFQ纯弯曲——梁弯曲时，各横截面上只有弯矩而无剪力的情况。48.4.2梁横截面上的正应力公式几何方面静力学方面应力计算公式导出物理方面8.4.2.1纯弯曲时的正应力5要找出梁横截面上正应力变化规律，须先找出纵向线应变在该截面上的变化规律。1、几何方面（中性轴）（对称轴）yz中性层a)c)b)MMMMd2211纵线横线x梁变形后现象：各横向线仍为直线,只倾斜一角度各纵向线弯成曲线,上部纵向线缩短,下部纵向线伸长纵向线伸长区梁宽减小;纵向线缩短区梁宽增大6由观察变形而得的假设:平面假设:横截面变形后仍保持平面,且仍垂直于变形后梁轴线,只绕横截面内某轴(中性轴)转一角度单向(纵向)受力假设:变形后各纤维之间互不挤压,只受拉伸或压缩作用.（中性轴）（对称轴）yz中性层a)c)b)MMMMd2211纵线横线x中性层中性层::梁内既不伸长也不缩短的纵向纤维层中性轴中性轴((zz轴轴):):中性层与各横截面的交线,垂直于横截面的对称轴y7x1122oo12abzy（中性轴）（对称轴）o'o'21a'b'1122θyρa)b)c)yddxd纵向纤维线应变变化规律:变形前：变形后:abab的的伸长量：量：abab的线应变的线应变::12ooabdx()abyd12oodxd()SabdxyddydSydydxd82、物理方面（弹性）EyE中性轴c)b)a)3、静力学方面(合力矩定理、合力定理)zAMydAM0yAMzdAyzMxAσzydNd0AFA922z1AAAzEMMydAydAIydAEI其中=00yAAAEMzdAzydAzydA推论1:中性轴必通过截面形心推论2:z轴为主惯性轴EIz—梁的弯曲刚度zzEyEyMMyEII正应力计算公式M—横截面上的弯矩y—所计算点到中性轴的距离Iz—截面对中性轴的惯性矩ZMyI00AAANydAydAEdAFyzMxAσzyd10最大正应力危险截面:最大弯矩所在截面Mmax危险点：距中性轴最远边缘点ymaxmaxmaxmaxzMyI令Iz/ymax=Wz,则max=Mmax/WzWz—弯曲截面系数应力正负号确定M为正时,中性轴上部截面受压下部截面受拉;M为负时,中性轴上部截面受拉下部截面受压.在拉区为正，压区为负11例6–7一简支梁及其所受荷载如图所示。若分别采用截面面积相同的矩形截面、圆形截面和工字形截面，试求以上三种截面梁的最大拉应力。设矩形截面高为140mm，宽为100mm，面积为140×100mm2。b)a)30（kNm）M＝20kN3m3mFCAB12解：kN·mmax30M(1)矩形截面22111(100140)66zWbhmm3=3.27×105mm33maxmax15913010()3.271010zMWPa=91.7MPa(2)圆形截面d=133.5mm3321ππ(133.5)3232zWdmm3=2.34×105mm33maxmax25923010()2.341010zMWPa=128.2MPab)a)30（kNm）M＝20kN3m3mFCAB13(3)工字形截面50C32080zWcm33maxmax3633010()208010zMWPa=14.4MPa以上计算结果表明，在承受相同荷载截面面积相同（即用料相同）的条件下，工字形截面梁所产生的最大拉应力最小，矩形次之，圆形最大。反过来说，使三种截面的梁所产生的最大拉应力相同时，工字梁所能承受的荷载最大。b)a)30（kNm）M＝20kN3m3mFCAB14例6-8一T形截面外伸梁及其所受荷载如图所示。试求最大的拉应力及最大的压应力。已知截面的惯性矩m4。6186.610zI60c)形心180Czy28060220Mb)4030＝20kN/m＝50kNC2m2mqABFD2ma)（kN.m）15解：MC=30kN·mMB=40kN·m60c)形心180Czy28060220Mb)4030＝20kN/m＝50kNC2m2mqABFD2ma)（kN.m）(1)B截面331max6401010010()186.610tBzMyI...