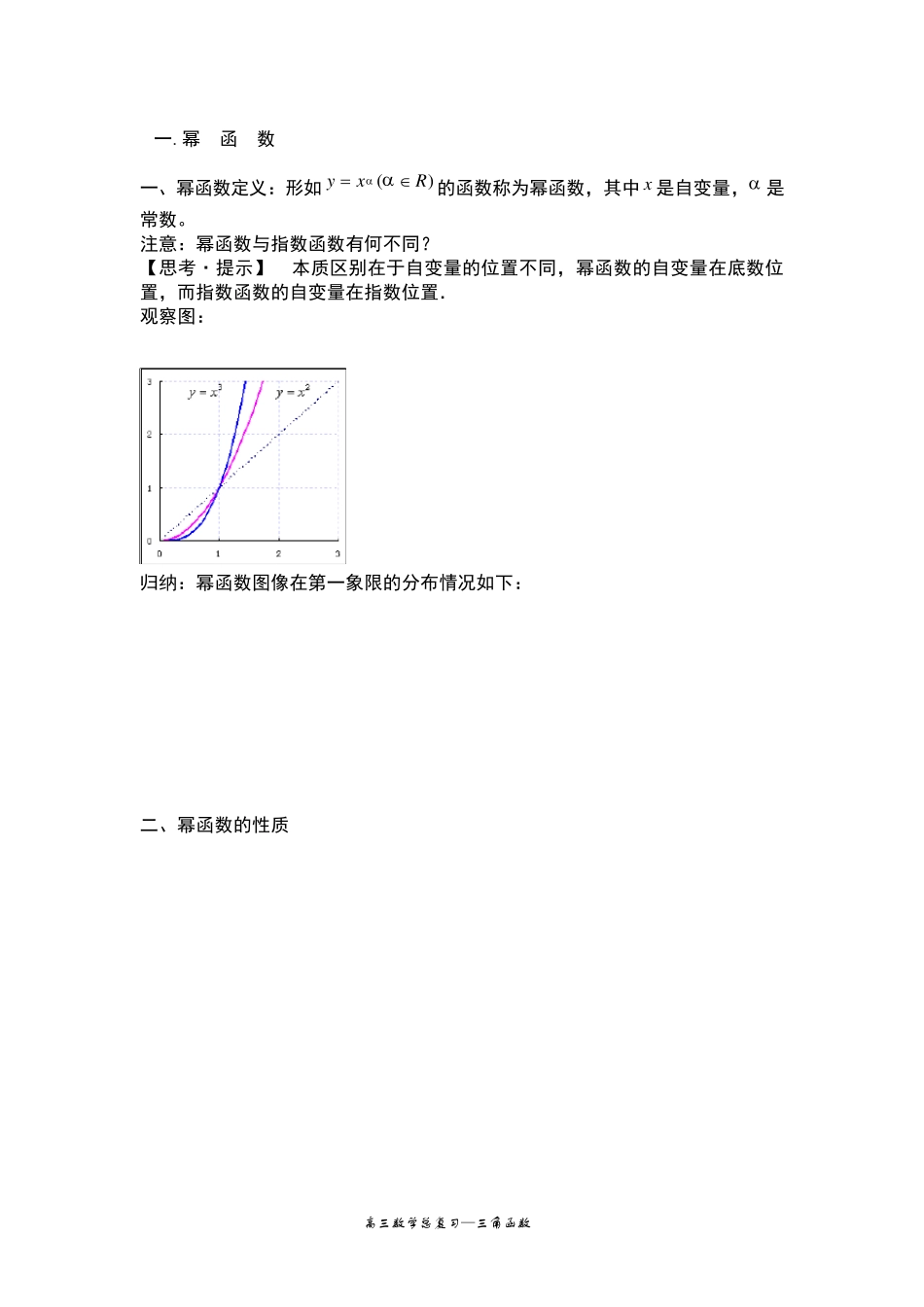
高三数学总复习—三角函数 一.幂 函 数 一、幂函数定义:形如)(Rxy的函数称为幂函数,其中x是自变量, 是常数。 注意:幂函数与指数函数有何不同? 【思考·提示】 本质区别在于自变量的位置不同,幂函数的自变量在底数位置,而指数函数的自变量在指数位置. 观察图: 归纳:幂函数图像在第一象限的分布情况如下: 二、幂函数的性质 高三数学总复习—三角函数 归纳:幂函数在第一象限的性质: 0,图像过定点(0,0)(1,1),在区间(,0)上单调递增。 0,图像过定点(1,1),在区间(,0)上单调递减。 探究:整数m,n 的奇偶与幂函数nmxy ),,,(互质且nmZnm的定义域以及奇偶性有什么关系? 结果:形如nmxy ),,,(互质且nmZnm的幂函数的奇偶性 (1)当m,n 都为奇数时,f(x)为奇函数,图象关于原点对称; (2)当m 为奇数n 为偶数时,f(x)为偶函数,图象关于y 轴对称; (3)当m 为偶数n 为奇数时,f(x)是非奇非偶函数,图象只在第一象限内. 三、幂函数的图像画法: 关键先画第一象限,然后根据奇偶性和定义域画其它象限。 指数大于1,在第一象限为抛物线型(凹); 指数等于1,在第一象限为上升的射线; 指数大于0 小于1,在第一象限为抛物线型(凸); 指数等于0,在第一象限为水平的射线; 指数小于0,在第一象限为双曲线型; 四、规律方法总结: 1、幂函数)1,0(xy的图像: 2、幂函数),,,,(互质qpZqppqxy的图像: 高三数学总复习—三角函数 3、比较幂形式的两个数的大小,一般的思路是: (1)若能化为同指数,则用幂函数的单调性; (2)若能化为同底数,则用指数函数的单调性; (3)若既不能化为同指数,也不能化为同底数,则需寻找一个恰当的数作为桥梁来比较大小. 二 . 指 数 与指 数 幂的运算 1. 根 式 的 概 念 : 一 般 地 , 如 果ax n , 那 么 x 叫 做 a 的 n 次 方根 , 其 中 n >1, 且 n ∈ N *. 负 数 没 有 偶 次 方 根 ; 0 的 任 何 次 方 根 都 是 0, 记 作00 n。 当n 是奇数时,aann ,当n 是偶数时,)0()0(||aaaaaann 2. 分 数 指 数 幂 正 数 的 分 数 指 数 幂 的 意 义 , 规 定 : )1,,,0(*nNnmaaanmnm)1,,,0(11*nNnmaaaanmnmnm 0 的 正 分 数 指 数 幂 等 ...