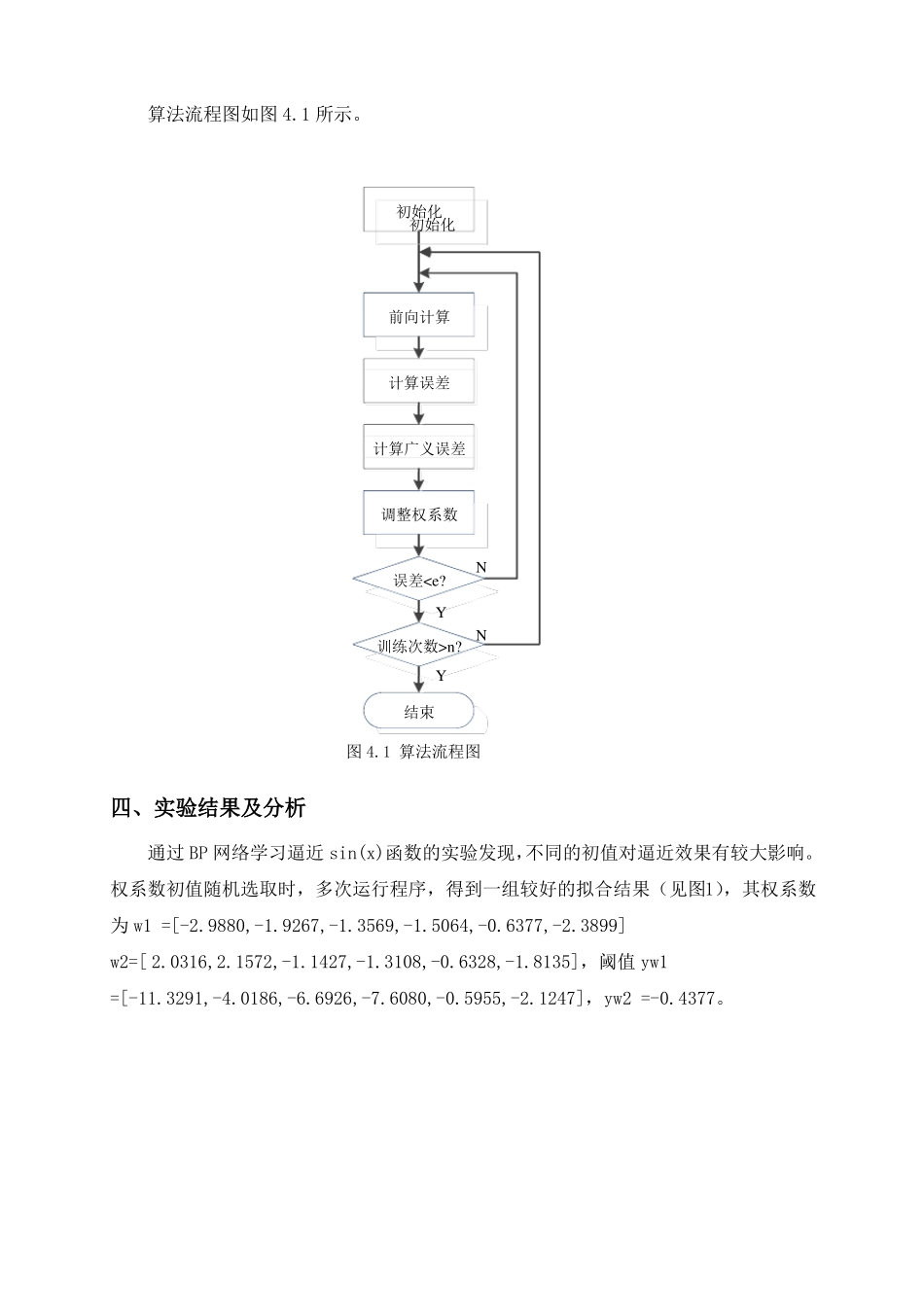
BP 神经网络用于函数拟合的实验一、实验目的本实验要求掌握前向型神经网络的基本工作原理及利用反向传播确定权系数的方法,并能在MATLAB 仿真环境下设计相应的神经网络,实现对非线性函数的逼近与拟合,并分析影响函数拟合效果的相关因素。二、实验要求设计神经网络的基本结构与激励函数,实现对非线性函数 y=sin(x)的逼近与拟合,并分析影响函数拟合效果的相关参数(包括激励函数的选择 sigmoid、线性函数、权系数的初值、步长的大小、训练样本的多少等),并对比实验效果。三、实验步骤1. 确定神经网络的结构本次实验采用前向型 BP 神经网络,神经元分层排列,每一层的神经元只接受前一层神经元的输入。输入模式经过各层的顺序变换后,得到输出层输出。各神经元之间不存在反馈。该实验神经网络含输入层和输出层两层神经元,其中输入层含六个神经元,输出层含一个神经元。输入信号传输到输入层,在输出层得到拟合结果。2. 确定采用的激励函数、拟合方法选择激励函数为 sigmoid 的函数,因其便于求导,且值域在(0,1)之间,具有较好的收敛特性。拟合方法采用梯度下降法,该方法使试验数值沿梯度方向增加有限步长,避免了盲目搜索,提高搜索效率。3. 训练流程1)初始化各参数2)开始训练3)计算误差4)计算广义误差5)调整连接权系数,直到误差小于设定值6)编写程序实现对非线性函数 y=sin(x)的逼近与拟合算法流程图如图 4.1 所示。初始化初始化前向计算计算误差计算广义误差调整权系数N误差n?Y结束N图 4.1 算法流程图四、实验结果及分析通过 BP 网络学习逼近 sin(x)函数的实验发现,不同的初值对逼近效果有较大影响。权系数初值随机选取时,多次运行程序,得到一组较好的拟合结果(见图1),其权系数为 w1 =[-2.9880,-1.9267,-1.3569,-1.5064,-0.6377,-2.3899]w2=[ 2.0316,2.1572,-1.1427,-1.3108,-0.6328,-1.8135],阈值 yw1=[-11.3291,-4.0186,-6.6926,-7.6080,-0.5955,-2.1247],yw2 =-0.4377。图 1固定选取初值为较好的拟合结果的权系数 w1,w2 及阈值 yw1,yw2,改变其学习步长,发现适当步长可以使网络拟合得更好,但过小及过大的步长都会加大误差(见图 2.1,图 2.2,图 2.3),图 2.1 设置的步长为 0.2,最终拟合误差在 0.1 左右,图 2.2 设置的步长为 0.02,最终拟合误差接近 0.02,图 2.3 设置的步长为 0.002,最终拟合误差在0.03 左右。由此可见,步长在 0.02 时,拟合得...