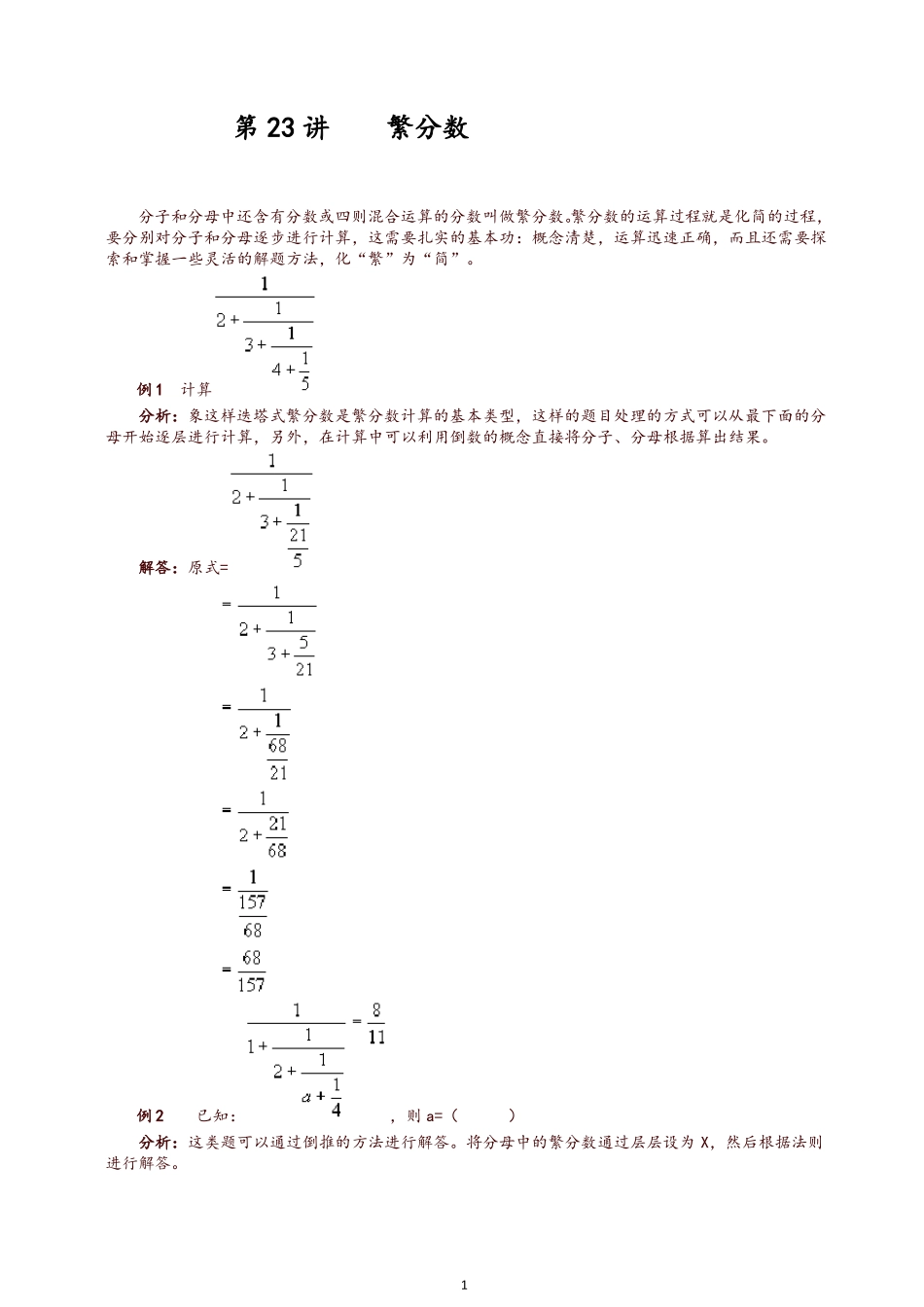
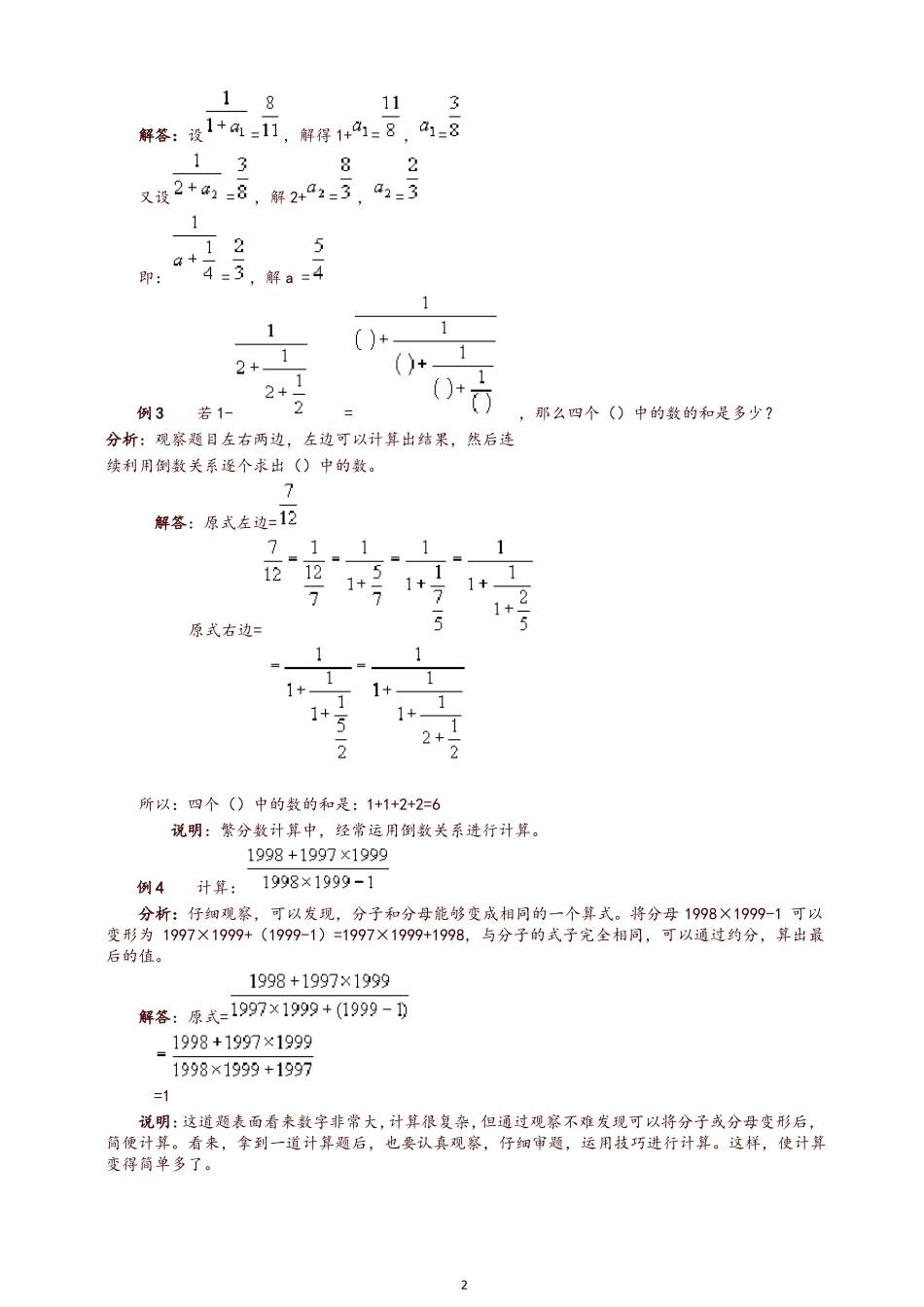
第 23 讲繁分数分子和分母中还含有分数或四则混合运算的分数叫做繁分数。繁分数的运算过程就是化简的过程,要分别对分子和分母逐步进行计算,这需要扎实的基本功:概念清楚,运算迅速正确,而且还需要探索和掌握一些灵活的解题方法,化“繁”为“简”。例 1计算分析:象这样迭塔式繁分数是繁分数计算的基本类型,这样的题目处理的方式可以从最下面的分母开始逐层进行计算,另外,在计算中可以利用倒数的概念直接将分子、分母根据算出结果。解答:原式=例 2已知:,则 a=()分析:这类题可以通过倒推的方法进行解答。将分母中的繁分数通过层层设为 X,然后根据法则进行解答。1解答:设=,解得 1+=,=又设=,解 2+=,=即:=,解 a =例 3若 1-=,那么四个()中的数的和是多少?分析:观察题目左右两边,左边可以计算出结果,然后连续利用倒数关系逐个求出()中的数。解答:原式左边=原式右边=所以:四个()中的数的和是:1+1+2+2=6说明:繁分数计算中,经常运用倒数关系进行计算。例 4计算:分析:仔细观察,可以发现,分子和分母能够变成相同的一个算式。将分母 1998×1999-1 可以变形为 1997×1999+(1999-1)=1997×1999+1998,与分子的式子完全相同,可以通过约分,算出最后的值。解答:原式==1说明:这道题表面看来数字非常大,计算很复杂,但通过观察不难发现可以将分子或分母变形后,简便计算。看来,拿到一道计算题后,也要认真观察,仔细审题,运用技巧进行计算。这样,使计算变得简单多了。2例 5分析:在这道题目中,分母都含有算式,我们不妨先将分母进行计算整理,看一看能不能发现规律。然后考虑运用一些计算的法则、技巧算出结果。解答:原式===2×(=2×(=2×()))=说明:有些题目一开始虽然看不出能利用简便方法进行计算,我们可以先按照计算的顺序进行计算整理,在计算过程中,随时发现可以简便计算时再进行简便计算。例如此题,开始时完全按照计算的方法将分母进行计算整理,然后,根据分数与除法的关系,将此题转变为分子是2 的繁分数,再根据乘法分配率,将 2 提出,再将括号中进行整理后,得到结果。例 6计算:分析:观察分子和分母,会发现它们有各自的规律可循。分母的数列排列的规律是从 1 加到 10再加回到 1,计算时只要计算(1+2+…+10)×2 再减 10,分子的规律注意是两个和相减,可以根据减法性质将括号打开进行计算。解答:分母=(1+2+3+…+10)×2-10=100分子=2==(2-1)(2+1)+(4-...