76第六节空间向量及其运算(理)练习题(2015年高考总复习)

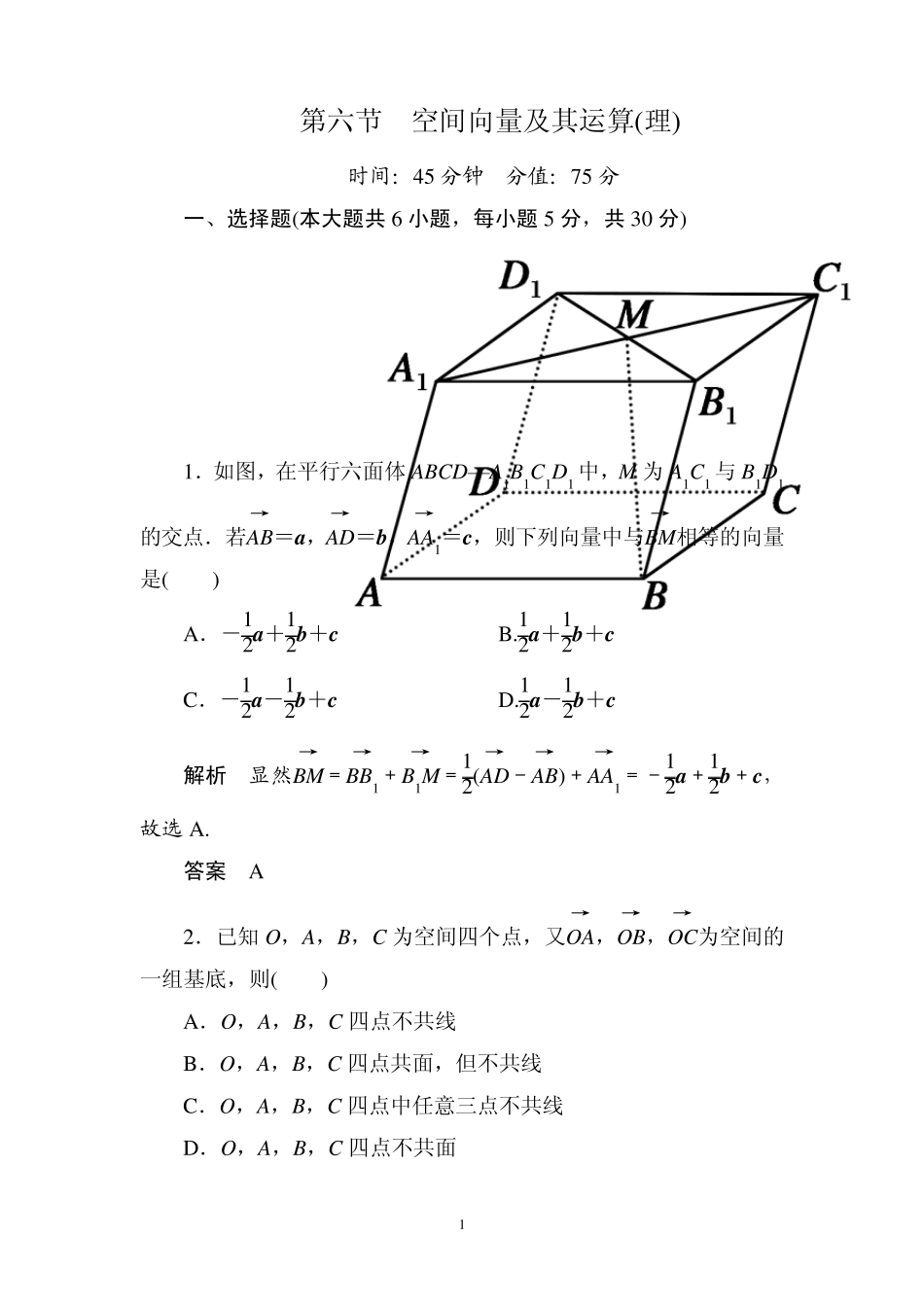
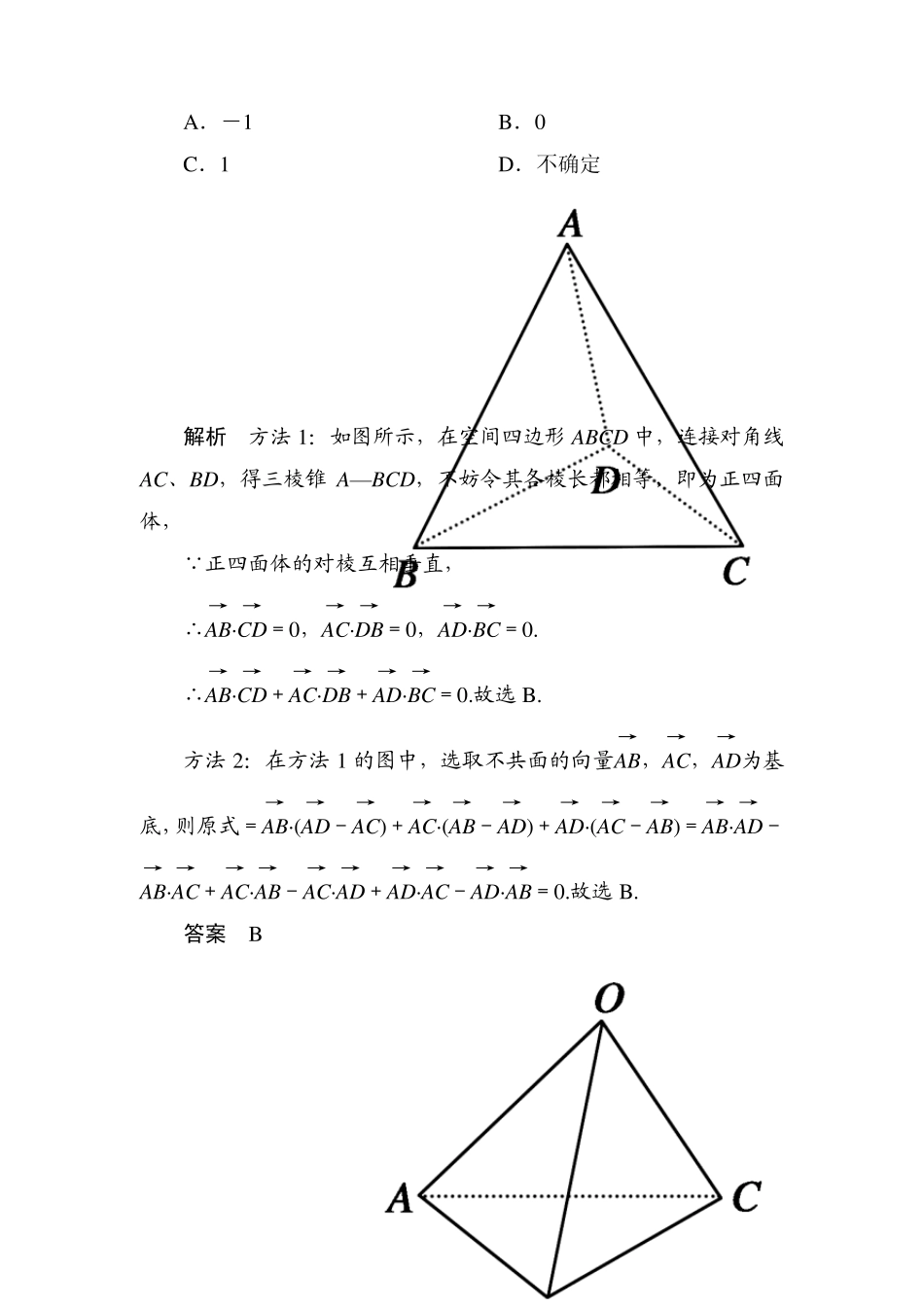
1 第六节 空间向量及其运算(理) 时间：45 分钟 分值：75 分 一、选择题(本大题共 6 小题，每小题 5 分，共 30 分) 1．如图，在平行六面体ABCD—A1B1C1D1 中，M 为A1C1 与B1D1的交点．若AB→＝a，AD→＝b，AA1→＝c，则下列向量中与BM→相等的向量是( ) A．－12a＋12b＋c B.12a＋12b＋c C．－12a－12b＋c D.12a－12b＋c 解析 显然BM→＝BB1→＋B1M→＝12(AD→－AB→)＋AA1→＝－12a＋12b＋c，故选 A. 答案 A 2．已知 O，A，B，C 为空间四个点，又OA→，OB→，OC→为空间的一组基底，则( ) A．O，A，B，C 四点不共线 B．O，A，B，C 四点共面，但不共线 C．O，A，B，C 四点中任意三点不共线 D．O，A，B，C 四点不共面 2 解析 OA→，OB→，OC→为空间的一组基底，所以OA→，OB→，OC→不共面，但 A，B，C 三种情况都有可能使OA→，OB→，OC→共面． 答案 D 3．已知 a＝(2，－1,3)，b＝(－1,4，－2)，c＝(7,5，λ)，若 a，b，c 三个向量共面，则实数 λ 等于( ) A.627 B.637 C.647 D.657 解析 由于 a，b，c 三向量共面． 所以存在实数 m，n使得 c＝ma＋nb， 即有 7＝2m－n，5＝－m＋4n，λ＝3m－2n，解得 m＝337 ，n＝177 ，λ＝657 .故选 D. 答案 D 4．正方体不在同一表面上的两个顶点为 A(－1,2，－1)，B(3，－2,3)，则正方体的体积为( ) A．8 B．27 C．64 D．128 解析 由于 A，B 是正方体上不共面的两个顶点，则 A，B 必为正方体一对角线的两顶点，由于|AB|＝ －1－32＋2＋22＋－1－32＝4 3，故正方体的边长为4，体积为43＝64.故选 C. 答案 C 5．在空间四边形 ABCD 中，AB→·CD→＋AC→·DB→＋AD→·BC→等于( ) 3 A．－1 B．0 C．1 D．不确定 解析 方法1：如图所示，在空间四边形ABCD 中，连接对角线AC、BD，得三棱锥A—BCD，不妨令其各棱长都相等，即为正四面体， 正四面体的对棱互相垂直， ∴AB→·CD→＝0，AC→·DB→＝0，AD→·BC→＝0. ∴AB→·CD→＋AC→·DB→＋AD→·BC→＝0.故选 B. 方法2：在方法1 的图中，选取不共面的向量AB→，AC→，AD→为基底，则原式＝AB→·(AD→－AC→)＋AC→·(AB→－AD→)＋AD→·(AC→－AB→)＝AB→·AD→－AB→·AC→＋AC→·AB→－AC→·AD→＋AD→·AC→－AD→·AB→＝0.故选 B. 答案 B 4 6．如图所示，已知空间四边形OABC 中，|OB|＝|OC|，且∠AOB＝∠A...