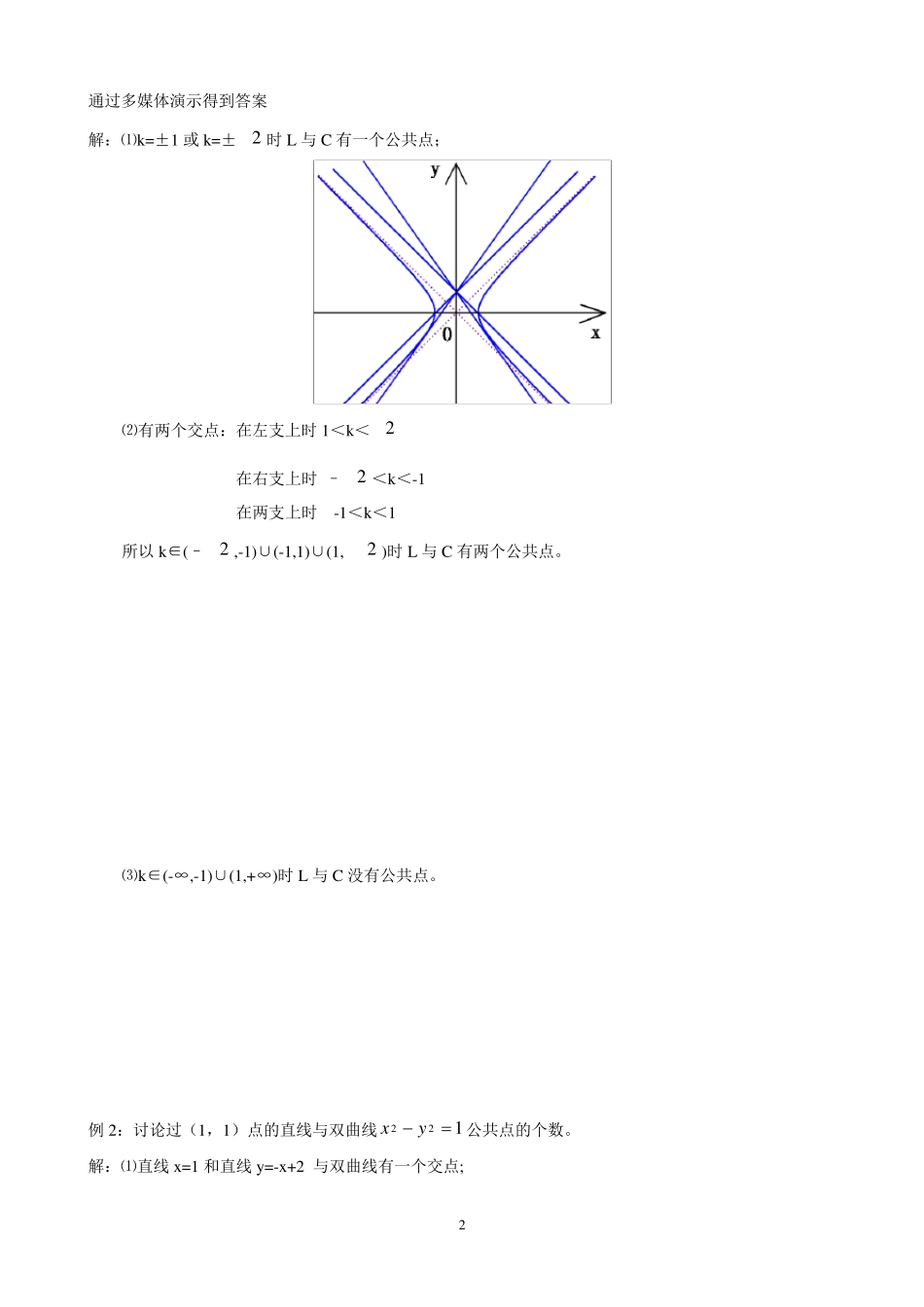
1 《直线和双曲线的交点个数问题》教学设计 昌黎汇文二中 李小庆 一、教学目的: 1.通过多媒体演示让学生掌握求直线与双曲线的交点个数的方法; 2.使学生认识到数形结合在解决问题中起到的重要作用。 二、教学重点和难点: 1. 直线与双曲线的交点个数的讨论; 2. 数形结合思想方法在解题中的应用 三、教学过程: 1、复习提问:双曲线的方程和性质 双曲线的标准方程 顶点 渐近线 焦点在x轴上 22221(0,0)xyabab 12(,0),( ,0)AaA a byxa 焦点在y轴上 22221(0,0)yxabab 12(,0),( ,0)BaB a ayxb 思考问题:求双曲线122 yx与下列直线的交点的个数: ①y=x+1 ②y= -x+1 ③12 xy ④12 xy ⑤y=1.2x+1 ⑥y= -1.2x+1 ⑦y=1 ⑧y=2x+1 ⑨y= -2x+1 老师提示:在求双曲线与直线的交点个数时,请说出它们的位置关系。 ① 与②的答案:1 直线与双曲线相交(直线与渐近线平行)。 ③与④的答案:1 直线与双曲线相切。 ⑤与⑥的答案:2 直线与双曲线相交,交点在一支上。 ⑦的答案:2 直线与双曲线相交,交点在两支上。 ⑧与⑨的答案:0 直线与双曲线相离。 (以上内容都有多媒体演示) 总结:当直线与双曲线相交(直线与渐近线平行)或直线与双曲线相切时直线与双曲线有一个公共点。 例 1:论直线y=kx+1 与双曲线C:122 yx公共点的个数。 分析:直线y=kx+1 过定点(0,1),解决这个问题的关键在于找什么?就是找与双曲线有一个交点的直线。 2 通过多媒体演示得到答案 解:⑴k=±1 或 k=±2 时 L 与 C 有一个公共点; ⑵有两个交点:在左支上时 1<k<2 在右支上时 –2 <k<-1 在两支上时 -1<k<1 所以 k∈(–2 ,-1)∪(-1,1)∪(1, 2 )时 L 与 C 有两个公共点。 ⑶k∈(-∞,-1)∪(1,+∞)时 L 与 C 没有公共点。 例 2:讨论过(1,1)点的直线与双曲线122 yx公共点的个数。 解:⑴直线 x=1 和直线 y=-x+2 与双曲线有一个交点; 3 ⑵k∈(-∞,-1) 时有两个交点在右支上; k∈(-1,1) 时有两个交点在两支上; ⑶k∈(1,+∞) 时没有公共点。 例 3:讨论直线 y=kx 与双曲线122 yx公共点的个数。 解:⑴没有和双曲线只有一个交点的直线; 4 ⑵k∈(-1,1) 时直线与双曲线有两个交点在两支上 ; ⑶k∈(-∞,-1)∪(1,+∞)时直线与双曲线没有公共点。 例4:讨论过(1,0)点的直线与双曲线122...