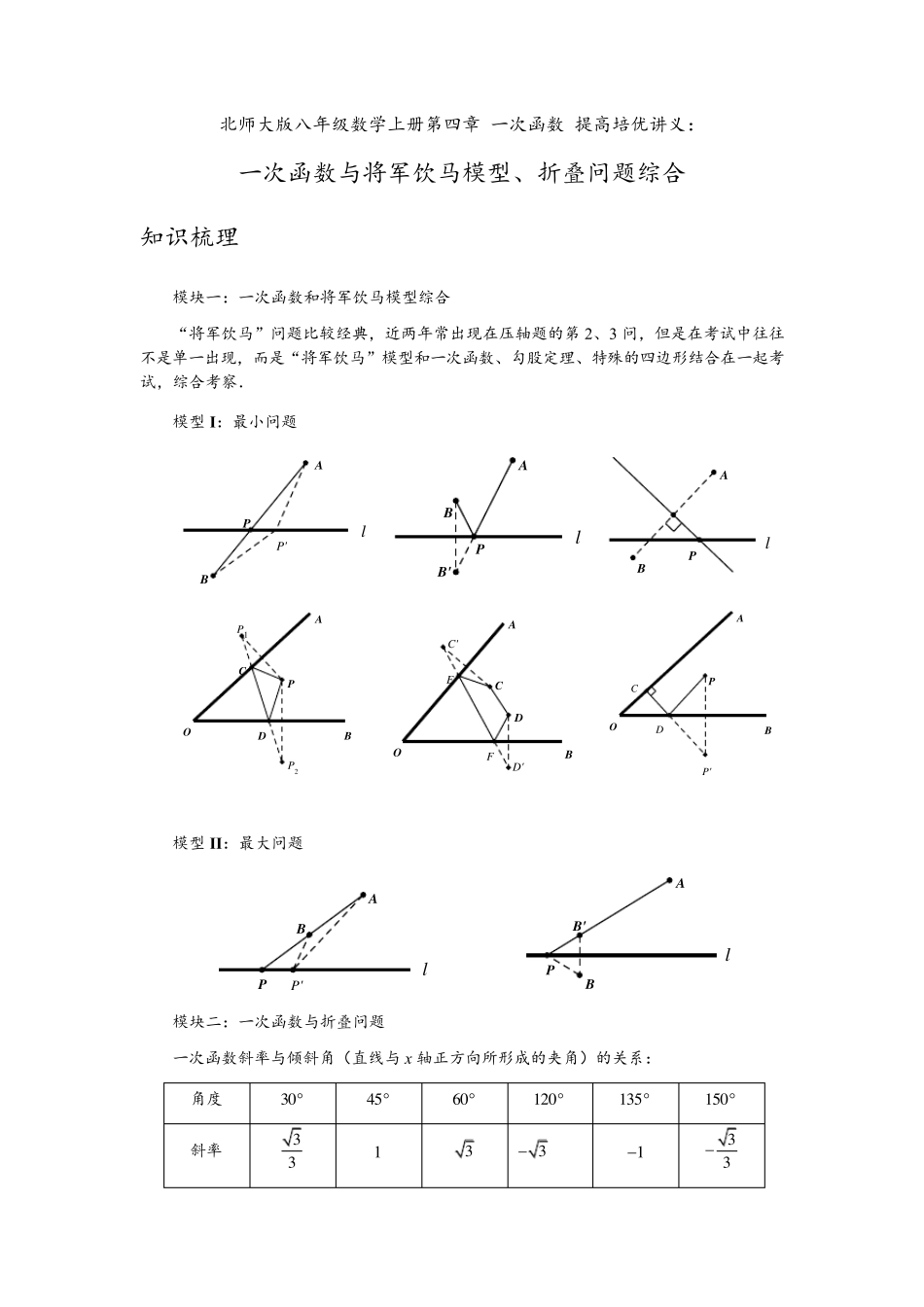
北师大版八年级数学上册第四章 一次函数 提高培优讲义: 一次函数与将军饮马模型、折叠问题综合 知识梳理 模块一:一次函数和将军饮马模型综合 “将军饮马”问题比较经典,近两年常出现在压轴题的第2、3 问,但是在考试中往往不是单一出现,而是“将军饮马”模型和一次函数、勾股定理、特殊的四边形结合在一起考试,综合考察. 模型I:最小问题 模型II:最大问题 模块二:一次函数与折叠问题 一次函数斜率与倾斜角(直线与x 轴正方向所形成的夹角)的关系: 角度 3 0 4 5 6 0 1 2 0 1 3 5 1 5 0 斜率 33 1 3 3 1 33 lP'PBAlB'PABPlABCDP2P1POBAFED'C'CDAOBDCP'PAOBlP'PABlB'PBA方法:解析法(根据折叠前后图像对称)、几何法(解直角三角形) 模块三:例题讲解 如图,已知ABC△三个顶点坐标分别为(0 , 4 )A,( 2 ,2 )B ,(3 , 0 )C,点 P 在线段 AC 上移动.当点 P 坐标为 (1 ,)m 时,请在 y轴上找点 Q,使PQC△周长最小,画出图形并求出 Q点坐标. 【解析】 (0 , 4 )A,(3 , 0 )C,∴直线 AC 的解析式为443yx ; 点 P 在线段 AC 上移动,点 P 坐标为(1, m),∴81 , 3P, 作 P 点关于 y轴的对称点 P′,连接 P C交 y轴于 Q,此时 PQQCP C , 根据两点之间线段最短,Q 就是使PQC△周长最小的点;则8'1 , 3P ∴直线 P′C 的解析式为223yx,∴Q 点的坐标为(0 , 2 ) . 【提示】这道题主要考查最一般的将军饮马,基本思路: (1)过定点作定直线的对称点; (2)作对称的目的是转移线段. 如图,在直角坐标系中有四个点( 6 , 3 )A ,( 2 , 5 )B ,(0 ,)Cm ,( , 0 )D n,当四边形 ABCD周长最短时,则 mn __________,此时四边形 ABCD 的面积为__________. xyCPAOB xyCPAOBP'Q 【解析】作A 点关于x 轴对称点A,作B 点关于y 轴对称点B,连接A D,B C. 四边形ABCD 周长最短,且AB 长度一定, ∴必须使 ADCDBC最短,即 A、D、C、 B共线,设直线 A B 为 ykxb,则( 6, 3)A' ,(2,5)B',将其代入直线中得:1k ,3b ,∴3yx , (0,)Cm ,( , 0)D n, 则代入直线方程中,得:3m ,3n , 因此, 0mn,通过四个点坐标易求出四边...