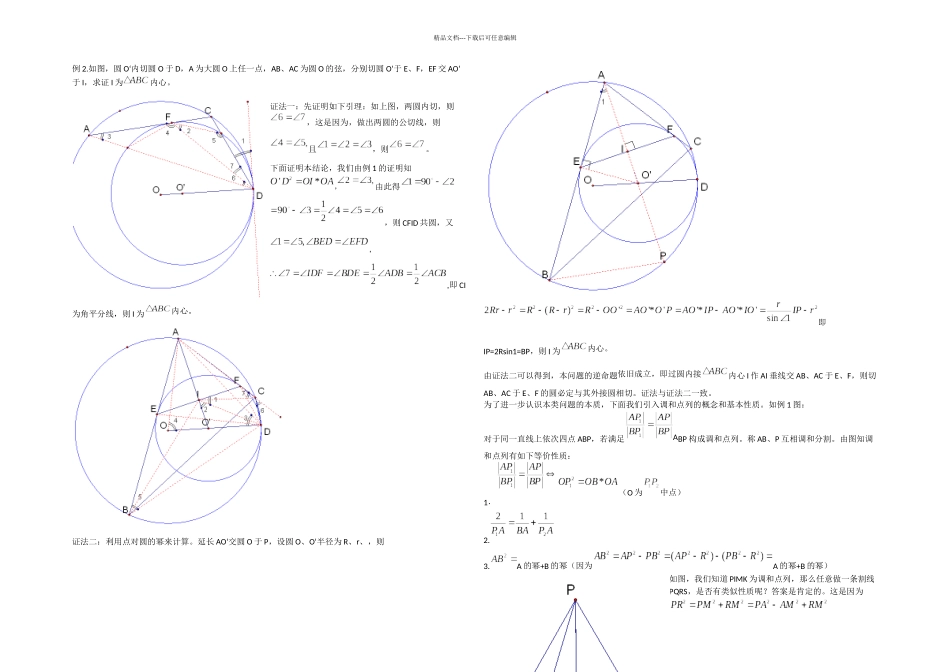
精品文档---下载后可任意编辑我们知道,到一点的距离为定长的点的轨迹是圆,到两定点距离之和为定值的点的轨迹是椭圆,到两定点距离之差为定值的点的轨迹是双曲线,那么到两定点距离之比为定值的点的轨迹是什么呢?求到两点距离之比为定值的点的轨迹。(为方便,我们设比值为 2.)我们可以用解析法做:设各点坐标如下则,这点的轨迹为圆心为的圆。我们当然也可以用几何法解。如图,设则我们首先在 AB 直线上确定满足此条件的点,显然内部外部各有一点满足条件然后设 P 点为轨迹上一点,则连接,由知分别为中 P 的内外角平分线,显然,即 P 点的轨迹为以为直径的圆。如图所示。一般的,到两定点距离之比为定值 k()的点的轨迹为圆,我们称为 Apolonius 圆,为古希腊数学家 Apolonius 最先提出并解决。他在许多问题中有重要应用。例 1.如图,过圆 O 外一点 P 作其切线 PA、PB,OP 与圆和 AB 分别交于 I、M,DE 为过 M 的任意弦。求证:I为内心。分析:当然要用内心定义证明 I 为角分线交点。证法 1:由垂直和射影定理及相交弦定理有:EM*MD==OM*MP,故 PDOE 四点共圆,又 OD=OE,则,即直线PD、PE 关于 PO 对称,则截弧相等,即 DI 平分,则 I 为内心,证毕。证法 2:容易发现本题本质即为 Apollonius 圆。因为如下图所示,我们刚才已经证完到 AB 距离之比为定值的点的轨迹为 Apollonius 圆。显然当时,有,则 AP 为圆切线,因此本题中圆为阿氏圆,则 PI、EI 分别为内角平分线,即 I 为内心。通过证法二说明发现问题的本质往往能轻而易举解决问题,而且还能更一步加深对问题的理解和把握。进一步,我们有过 M 的任意弦与 P 构成的三角形有共同的内心 I,反之呢?即若共一条角分线的两个三角形PAB、PDE 共内心 I,则四顶点 ADBE 共圆。由上面定理易得。如下图所示。顺便说一下,显然他们也共旁心。通过上例我们发现本定理的本质是一个比例关系式:精品文档---下载后可任意编辑例 2.如图,圆 O‘内切圆 O 于 D,A 为大圆 O 上任一点,AB、AC 为圆 O 的弦,分别切圆 O’于 E、F,EF 交 AO’于 I,求证 I 为内心。证法一:先证明如下引理:如上图,两圆内切,则,这是因为,做出两圆的公切线,则且,则。下面证明本结论,我们由例 1 的证明知,由此得,则 CFID 共圆,又,,即 CI为角平分线,则 I 为内心。证法二:利用点对圆的幂来计算。延长 AO‘交圆 O 于 ...