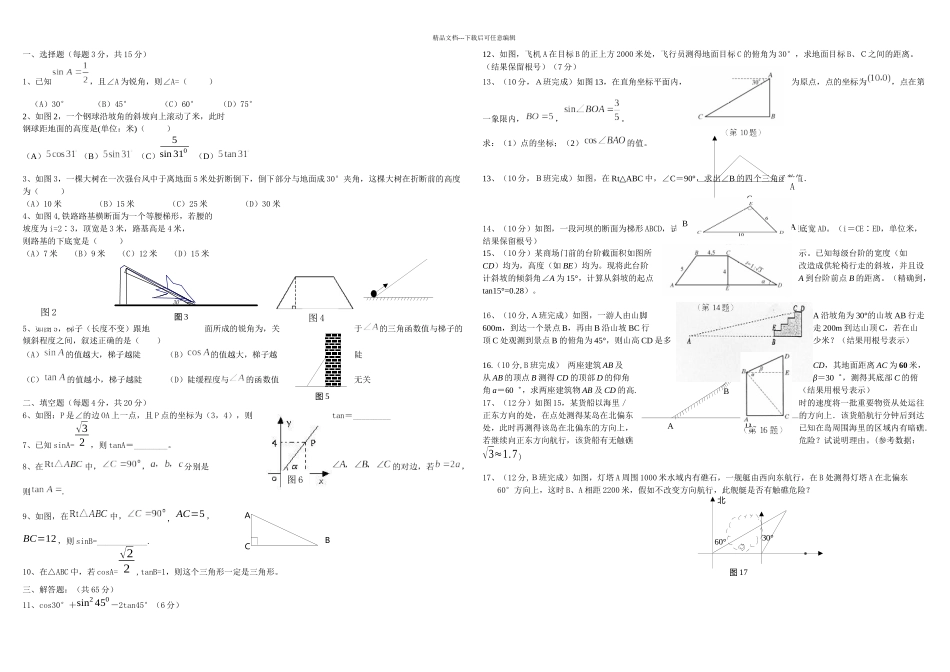
30°图 3图 5CAB图 13ABCD图 17北60°30°精品文档---下载后可任意编辑一、选择题(每题 3 分,共 15 分)1、已知,且∠A 为锐角,则∠A=( )(A)30° (B)45° (C)60° (D)75°2、如图 2,一个钢球沿坡角的斜坡向上滚动了米,此时钢球距地面的高度是(单位:米)( )(A)(B)(C)5sin 310(D)3、如图 3,一棵大树在一次强台风中于离地面 5 米处折断倒下,倒下部分与地面成 30°夹角,这棵大树在折断前的高度为( )(A)10 米 (B)15 米 (C)25 米 (D)30 米4、如图 4,铁路路基横断面为一个等腰梯形,若腰的坡度为 i=2∶3,顶宽是 3 米,路基高是 4 米,则路基的下底宽是( )(A)7 米 (B)9 米 (C)12 米 (D)15 米5、如图 5,梯子(长度不变)跟地面所成的锐角为,关于的三角函数值与梯子的倾斜程度之间,叙述正确的是( )(A)的值越大,梯子越陡(B)的值越大,梯子越陡(C)的值越小,梯子越陡(D)陡缓程度与的函数值无关二、填空题(每题 4 分,共 20 分)6、如图:P 是∠的边 OA 上一点,且 P 点的坐标为(3,4),则tan=_________7、已知 sinA=√32 ,则 tanA=________。8、在中,,分别是的对边,若,则.9、如图,在中,,AC=5 ,BC=12 ,则 sinB=____________.10、在△ABC 中,若 cosA=√22 ,tanB=1,则这个三角形一定是三角形。 三、解答题:(共 65 分)11、cos30°+sin2 450 -2tan45°(6 分)12、如图,飞机 A 在目标 B 的正上方 2000 米处,飞行员测得地面目标 C 的俯角为 30°,求地面目标 B、C之间的距离。(结果保留根号)(7 分)13、(10 分,A班完成)如图 13,在直角坐标平面内,为原点,点的坐标为,点在第一象限内,,。求:(1)点的坐标;(2)的值。13、(10 分,B班完成)如图,在 Rt ABC△中,∠C=90°,求出∠B 的四个三角函数值.14、(10 分)如图,一段河坝的断面为梯形 ABCD,试根据图中数据,求出坡角 α 和坝底宽 AD。(i=CE∶ED,单位米,结果保留根号)15、(10 分)某商场门前的台阶截面积如图所示。已知每级台阶的宽度(如CD)均为,高度(如 BE)均为。现将此台阶改造成供轮椅行走的斜坡,并且设计斜坡的倾斜角∠A 为 15°,计算从斜坡的起点A 到台阶前点 B 的距离。(精确到,tan15°=0.28)。16、(10 分,A班完成)如图,一游人由山脚A 沿坡角为 30°的山坡...