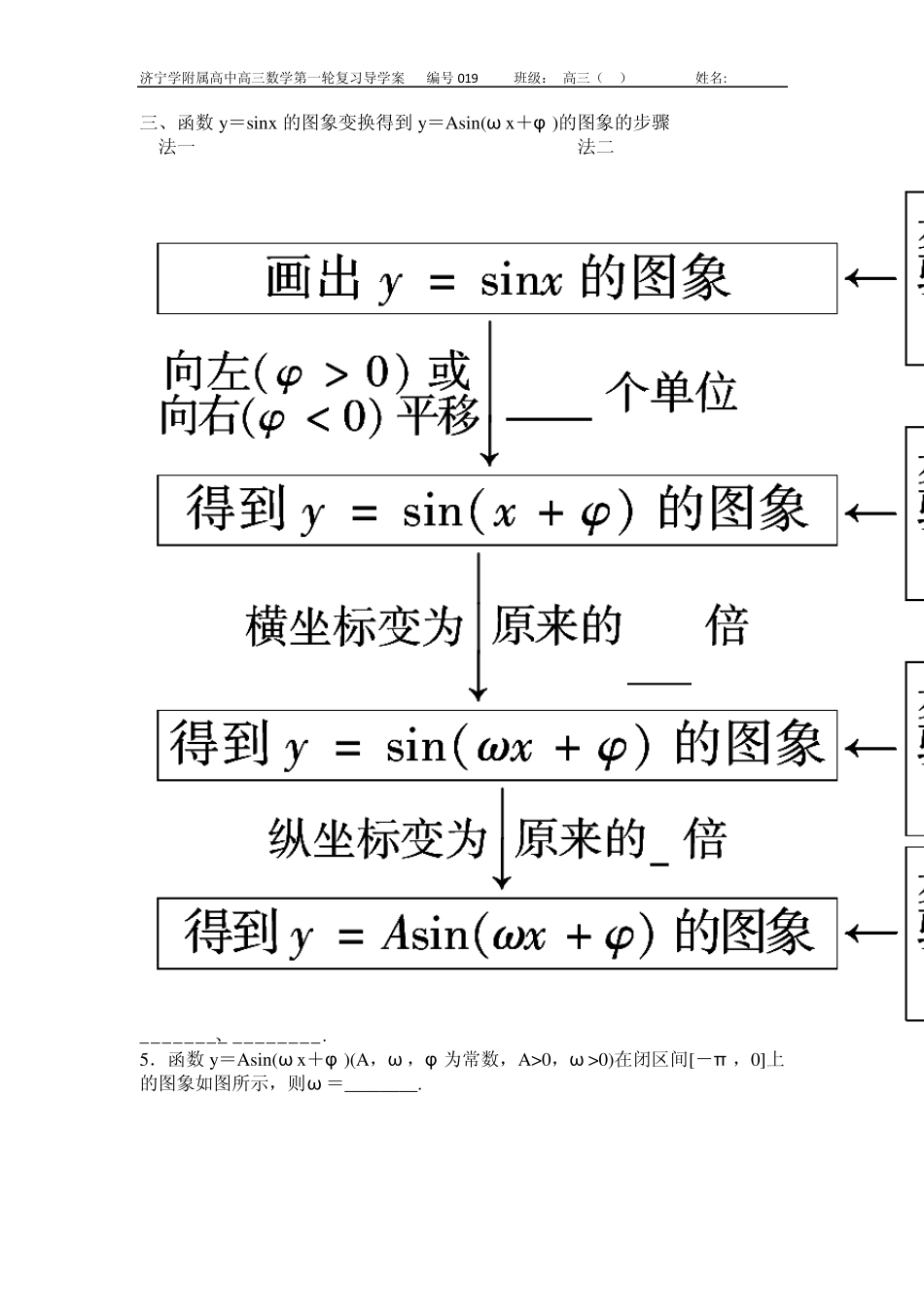
济宁学附属高中高三数学第一轮复习导学案 编号019 班级: 高三( ) 姓名: 函数y=Asin(ω x+φ )的图象及三角函数模型的简单应用 考纲要求 1.了解函数y=Asin(ω x+φ )的物理意义,能画出函数y=Asin(ω x+φ )的图象,了解参数A、ω 、φ 对函数图象变化的影响. 2.会用三角函数解决一些简单实际问题. 考情分析 1.“五点法” 作图及图象的变换是考查的重点. 2.结合三角恒等变换考查y=Asin(ω x+φ )的性质及简单 应用是考查的热点. 教学过程: 基础梳理 一、y=Asin(ω x+φ )的有关概念 y=Asin(ω x+φ )(A>0,ω >0), x∈[0,+∞)表示一个振动量时 振幅 周期 频率 相位 初相 A T= f= = ω x+φ φ 二、用五点法画y=Asin(ω x+φ )一个周期内的简图 用五点法画y=Asin(ω x+φ )一个周期内的简图时,要找五个关键点,如下表所示. x ω x+φ 0 π2 π 2π y= Asin(ω x+φ ) 0 A 0 -A 0 济宁学附属高中高三数学第一轮复习导学案 编号019 班级: 高三( ) 姓名: 三、函数y=sinx 的图象变换得到y=Asin(ω x+φ )的图象的步骤 法一 法二 双基自测: 1.函数y =sinx2的图象的一条对称轴的方程是( ) A.x =0 B.x =π2 C.x =π D.x =2π 2.(教材习题改编)已知简谐运动f(x )=2sin π3x +φ (|φ|<π2)的图象经过点(0,1),则该简谐运动的最小正周期T 和初相φ 分别为( ) A.T=6,φ=π6 B.T=6,φ=π3 C.T=6π,φ=π6 D.T=6π,φ=π3 3.将函数y =sin x 的图象向左平移φ(0≤φ<2π)个单位后,得到函 数y =sin x -π6 的图象,则φ 等于 ( ) A.π6 B.11π6 C.7π6 D.5π6 4.(教材习题改编)y =2sin 2x -π4 的振幅为________,频率和初相分别为________、________. 5.函数y=Asin(ω x+φ )(A,ω ,φ 为常数,A>0,ω >0)在闭区间[-π ,0]上的图象如图所示,则ω =________. 济宁学附属高中高三数学第一轮复习导学案 编号 019 班级: 高三( ) 姓名: 关键点点拨: 3 1、 确定 y =Asin(ωx+φ)+k (A>0,ω>0,|φ|<π )中的参数方法 在由图象求解析式时,若最大值为 M,最小值为 m,则 A= M-m2 ,k=M+m2 ,ω由周期 T确定,即由2πω =T求出,φ 由特殊点确定. 2....