全等三角形及基本判定定理

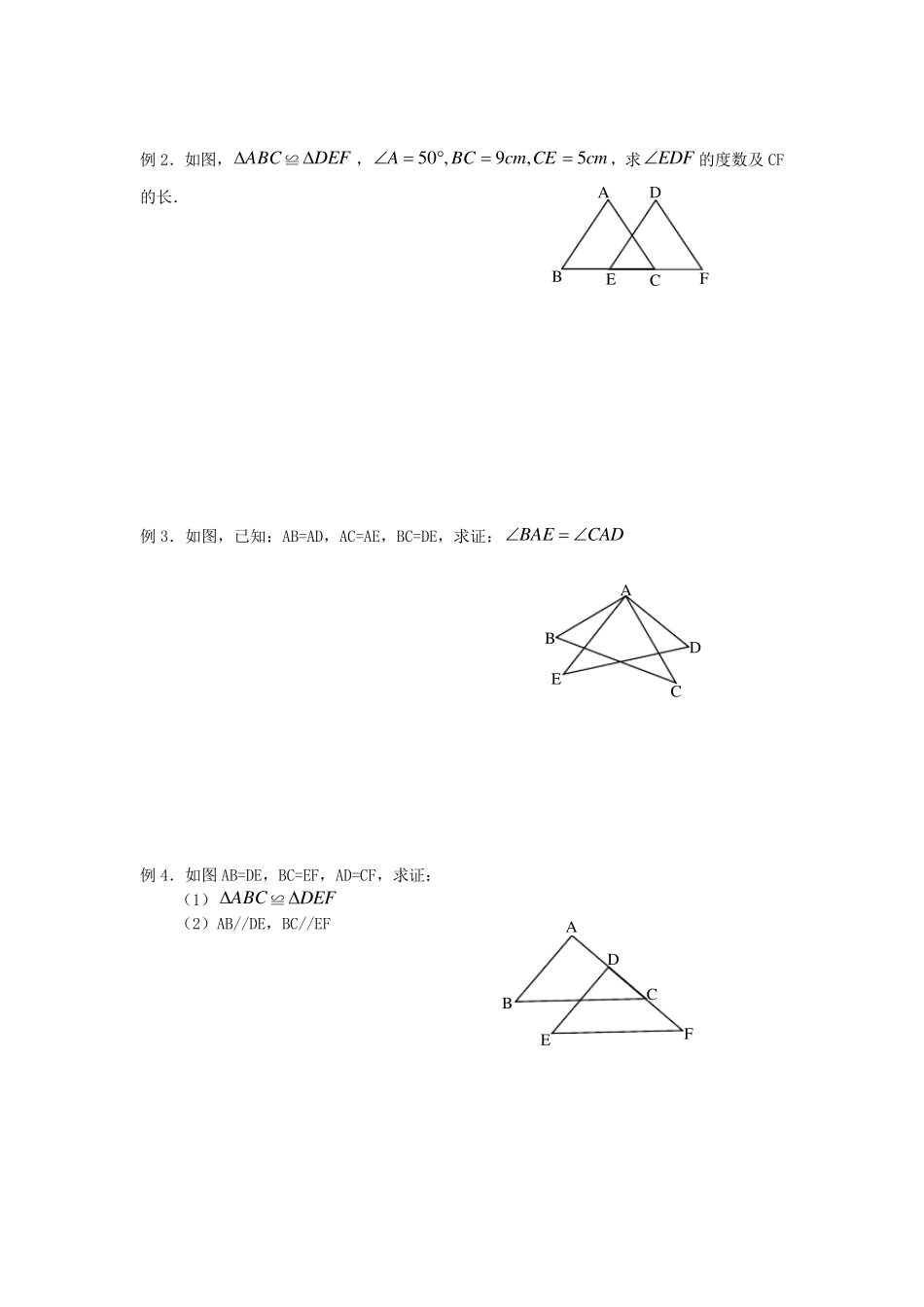
全等三角形 全 等 三 角 形 【知识要点】 1．全等图形定义：两个能够重合的图形称为全等图形． 2．全等图形的性质： （1）全等图形的形状和大小都相同，对应边相等，对应角相等 （2）全等图形的面积相等 3．全等三角形：两个能够完全重合的三角形称为全等三角形 （1）表示方法：两个三角形全等用符号“≌”来表示，读作“全等于” 如DEFABC与全等，记作 ABC≌ DEF （2）符号“≌”的含义：“∽”表示形状相同，“=”表示大小相等，合起来就是形状相同，大小也相等，这就是全等． （3）两个全等三角形重合时，互相重合的顶点叫做对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角． （4）证两个三角形全等时，通常把表示对应顶点的字母写在对应的位置上． 全等三角形的判定1：SSS 三边对应相等的两个三角形全等，简与成“边边边”或“SSS”． 如图，在 ABC和DEF中DFACEFBCDEAB ABC≌ DEF 【典型例题】 例 1．如图，ABC≌ ADC，点B 与点D 是对应点，26BAC，且20B，1ABCS，求ACDDCAD,,的度数及 ACD的面积． A B C D E F A B D C 例2．如图，ABC≌ DEF，cmCEcmBCA5,9,50，求EDF的度数及 CF的长． 例3．如图，已知：AB=AD，AC=AE，BC=DE，求证：CADBAE 例4．如图AB=DE，BC=EF，AD=CF，求证： （1） ABC≌ DEF （2）AB//DE，BC//EF A B E C F D A B E C D A B C D F E 例5．如图，在,90CABC中D、E 分别为AC、AB 上的点，且BE=BC，DE=DC，求证：（1） ABDE ； （2）BD 平分ABC （角平分线的相关证明及性质） 全等三角形判定定理2：SAS 两边和它们的夹角对应相等的两个三角形全等，简写成“边角边”或“SAS”。 几何表示 如图，在ABC和DEF中 ABCEFBCEBDEAB≌)(SASDEF 【典型例题】 【例1】 已知：如图，AB=AC，AD=AE，求证：BE=CD. A E B C D A B C E D F A D B E C 【例2】 如图，已知：点D、E 在BC 上，且BD=CE，AD=AE，∠1=∠2，由此你能得出哪些结论？给出证明. 【例3】 如图已知：AE=AF，AB=AC，∠A=60°，∠B=24°，求∠BOE 的度数. 【例4】 如图，B，C，D 在同一条直线上，△ABC，△ADE 是等边三角形， 求证：①CE=AC+DC； ②∠ECD=60°. 【例5】如图，已知△ABC、△BDE 均为等...