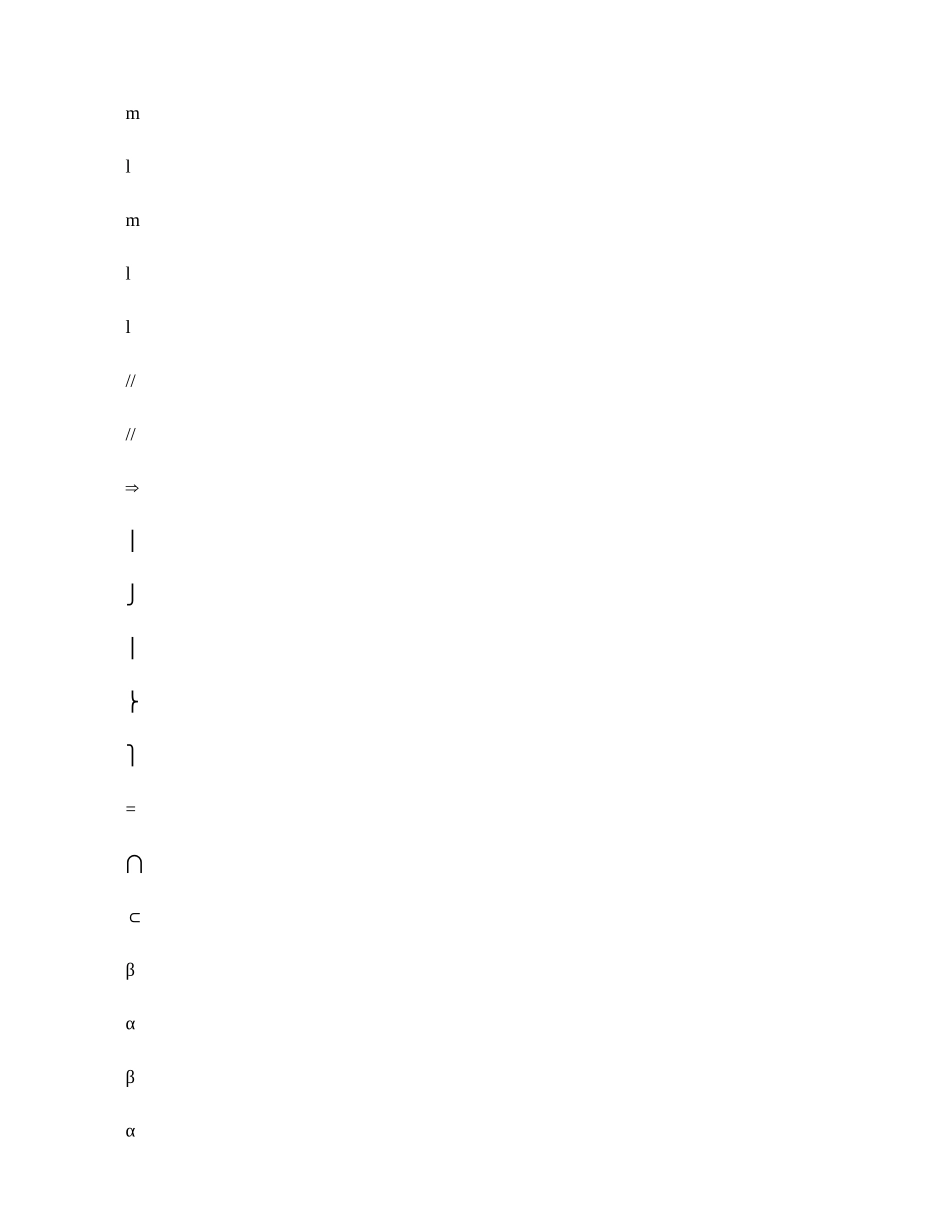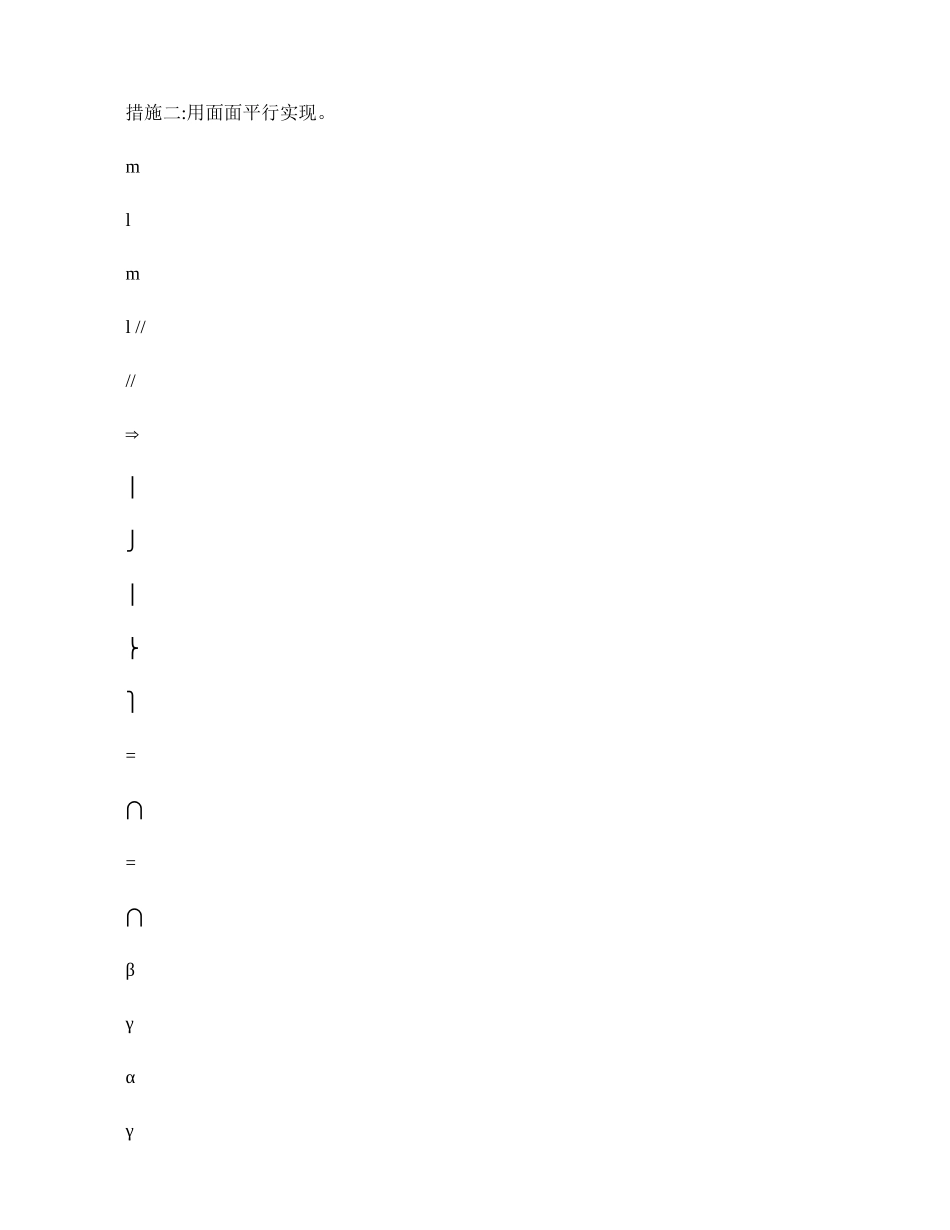立体几何知识点整理姓名: 一.直线和平面的三种位置关系:1. 线面平行l符号表达:2. 线面相交 符号表达: 3. 线在面内符号表达:二.平行关系:1. 线线平行:措施一:用线面平行实现。mlmll////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα措施二:用面面平行实现。mlml ////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα措施三:用线面垂直实现。 若 αα⊥m⊥l , , 则 ml //。措施四:用向量措施: 若向量 和向量 共线且 l 、 m 不重叠, 则 ml //。2. 线面平行:措施一:用线线平行实现。ααα////llmml⇒⎪⎭⎪⎬⎫⊄⊂措施二:用面面平行实现。αββα////ll⇒⎭⎬⎫⊂措施三:用平面法向量实现。 若 n 为平面 α 的一种法向 量 , ln ⊥ 且 α⊄l , 则 α//l 。3. 面面平行:措施一:用线线平行实现。βααβ// ', ','//'//⇒⎪⎪⎭⎪⎪⎬⎫⊂⊂且相交且相交mlmlmmll措施二:用线面平行实现。βαβαα// ,////⇒⎪⎭⎪⎬⎫⊂且相交mlml三.垂直关系:1. 线面垂直:措施一:用线线垂直实现。αα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥lABACAABACABlACl,ml 措施二: 用面面垂直实现。 αββαβα⊥⇒⎪⎭⎪⎬⎫=l l m l m ,⊂⊥⊥⋂2. 面面垂直:措施一:用线面垂直实现。βαβα⊥⇒⎭⎬⎫l l⊂⊥措施二: 计算所成二面角为直角。 3. 线线垂直:措施一:用线面垂直实现。m l m l ⊥⇒⎭⎬⎫αα⊂⊥措施二:三垂线定理及其逆定理。PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⊂⎬⎪⎭措施三:用向量措施: 若向量 和向量 的数量积为 0, 则 m l ⊥ 。 三. 夹角问题。 ( 一 异 面直线所成的角: (1 范围:]90, 0( (2︒︒求法: 措施一:定义法。 环节 1:平移,使它们相交,找到夹角。 环节 2: 解三角形求出角。 ( 常用到余弦定理 余弦定理:abcb a 2cos 222-+=θ( 计算成果也许是其补角措施二: 向量法。转化为向量的夹角 ( 计算成果也许是其补角 : =θcos( 二 线 面角(1 定义: 直线 l 上任取一点 P ( 交点除外 , 作 PO ⊥α 于 O, 连结 AO , 则 AO 为斜线 PA 在面 α 内 的射影, PAO (∠ 图中 θ 为直线 l 与面 α 所成的角。 (2 范围:]90, 0[︒︒ 当 ︒=0θ 时, αl ⊂ 或 α//l 当 ︒=90θ 时, αl (3⊥求法: 措施一:定义法。 环节 1:作出线面角, 并证明。 环节 2:解三角形,求出线面角。措施二: 向量法 ( 为平面 α 的一种法向量 。><=, cos sin ...