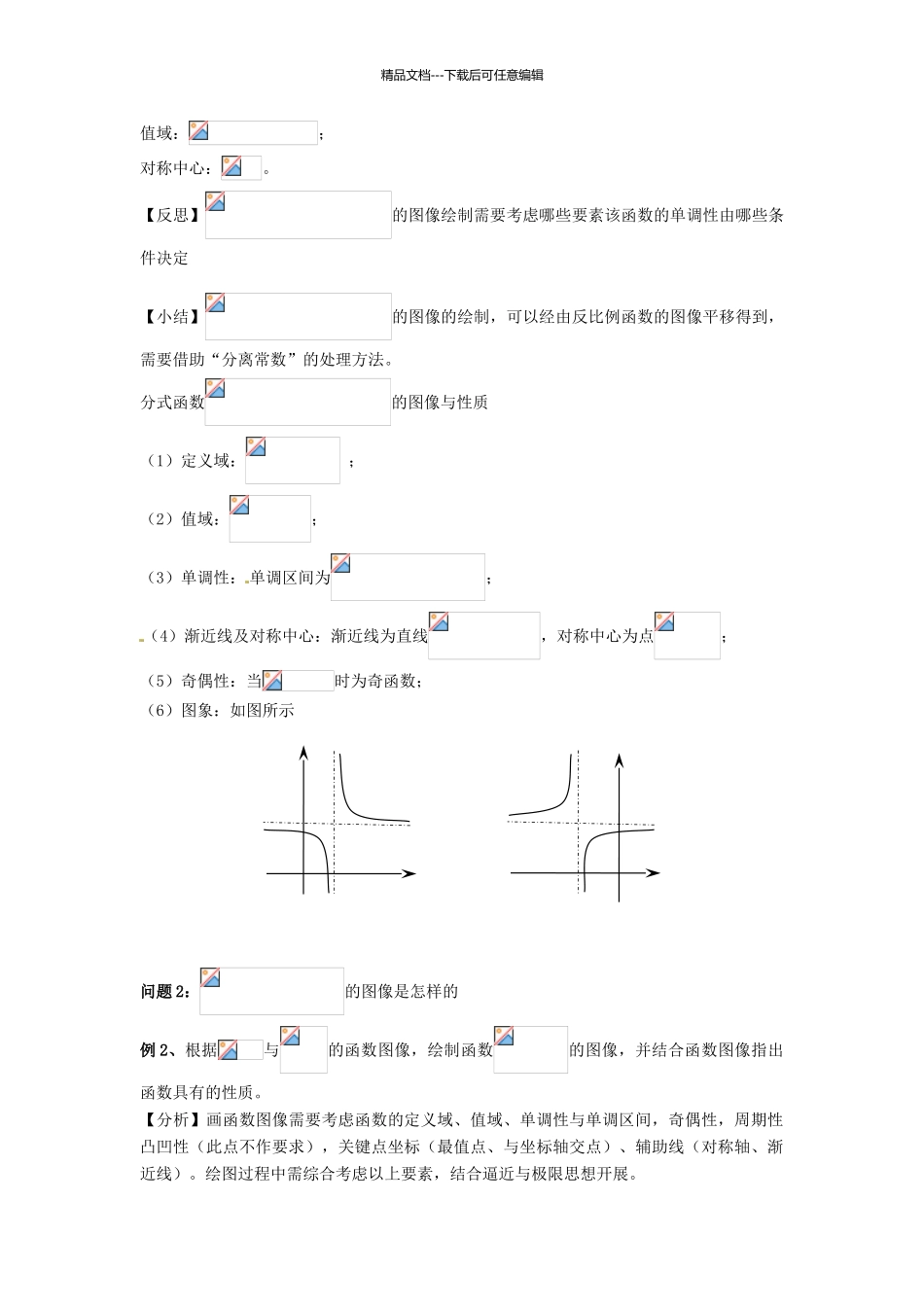
精品文档---下载后可任意编辑分式函数的图像与性质 学习过程 1、分式函数的概念形 如的 函 数 称 为 分 式 函 数 。 如,,等。2、分式复合函数形如的函数称为分式复合函数。如,,等。※ 学习探究探究任务一:函数的图像与性质问题 1:的图像是怎样的例 1、画出函数的图像,依据函数图像,指出函数的单调区间、值域、对称中心。【分析】,即函数的图像可以经由函数的图像向右平移 1 个单位,再向上平移 2 个单位得到。如下表所示:由此可以画出函数的图像,如下:单调减区间:;精品文档---下载后可任意编辑值域:;对称中心:。【反思】的图像绘制需要考虑哪些要素该函数的单调性由哪些条件决定【小结】的图像的绘制,可以经由反比例函数的图像平移得到,需要借助“分离常数”的处理方法。分式函数的图像与性质 (1)定义域: ;(2)值域:;(3)单调性: 单调区间为;(4)渐近线及对称中心:渐近线为直线,对称中心为点;(5)奇偶性:当时为奇函数;(6)图象:如图所示问题 2:的图像是怎样的例 2、根据与的函数图像,绘制函数的图像,并结合函数图像指出函数具有的性质。【分析】画函数图像需要考虑函数的定义域、值域、单调性与单调区间,奇偶性,周期性凸凹性(此点不作要求),关键点坐标(最值点、与坐标轴交点)、辅助线(对称轴、渐近线)。绘图过程中需综合考虑以上要素,结合逼近与极限思想开展。精品文档---下载后可任意编辑解:函数的定义域为:;根据单调 性定义,可以求出的单调区间增区间:减区间:函数的值域为:函数的奇偶性:奇函数函数图像的渐近线为:函数的图像如下:【反思】如何绘制陌生函 数的图像讨论新函数性质应从哪些方面入手【小结】分式函数的图像与性质:(1)定义域:;(2)值域:;(3)奇偶性:奇函数;(4)单调性:在区间上是增函数,在区间上为减函数;(5)渐近线:以轴和直线为渐近线;(6)图象:如右图所示精品文档---下载后可任意编辑例 3、根据与的函数图像,绘制函数的图像,并结合函数图像指出函数具有的性质。【分析】结合刚才的绘图经验,不难绘制出的图像解:函数的定义域为:;根据单调性定义,可以推断出的单调性,单调增区间为:精品文档---下载后可任意编辑函数的值域为:函数的奇偶性:奇函数函数图像的渐近线为:函数的图像如下:【反思】结合刚才的两 个例子, 与的图像又是怎样的呢 思考与的图像是怎样的呢的图像呢函数的图像如下,绘制的过程可...