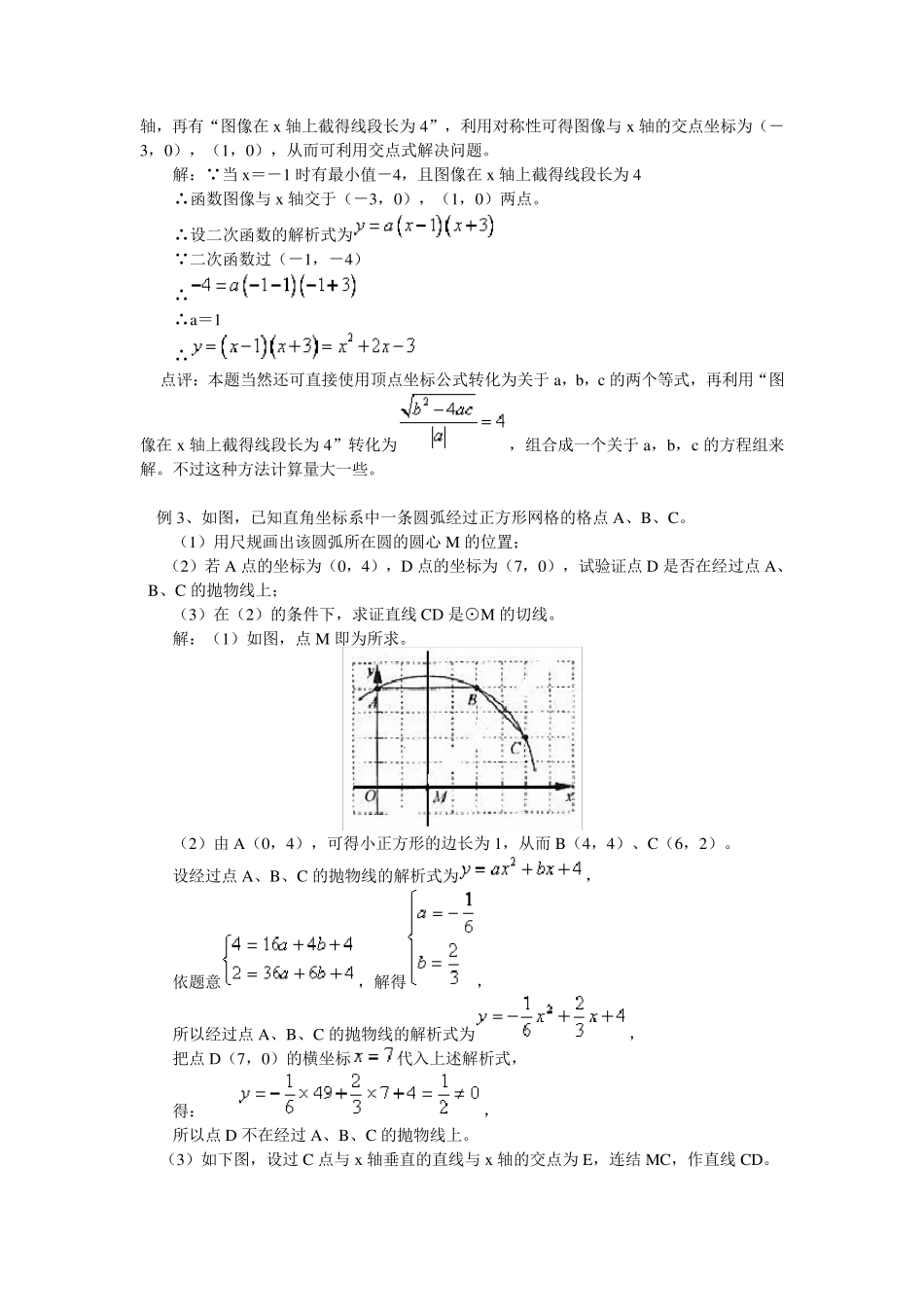
抛物线的解析式的三种形式 抛物线的解析式有三种形式: ①一般式:(a≠0); ②顶点式:,(h,k)是顶点坐标; ③交点式:(a≠0),其中x1,x2 是方程的两个实根。 在实际应用中,需要根据题目的条件选择相应的形式以简化计算。 利用待定系数法确定二次函数的解析式的步骤可以总结为五个字:设、列、求、定。 例 1、已知二次函数图像顶点坐标为(-2,3),且过点(1,0),求此二次函数的解析式。(试用两种不同的方法) 分析:根据所给条件中有顶点坐标的特点,可以选用顶点式。 解法一: 设二次函数的解析式为: 因为二次函数图像过点(1,0) 所以 所以 所以函数解析式为。 分析:根据所给条件中顶点坐标可知,抛物线的对称轴为x=-2,利用抛物线的对称性,可求得点(1,0)关于对称轴 x=-2 的对称点(-5,0),可选用交点式。 解法二: 设二次函数的解析式为:, 因为二次函数图像过点(-2,3) 所以 所以函数解析式为。 点评:当题目条件中有顶点坐标时,选用顶点式;当条件中有两个与 x 轴的交点时,一般选用交点式。但我们注意到,解法二是在知道抛物线与 x 轴的一个交点后,利用对称轴可从顶点坐标中得到,再利用抛物线的对称性获得另外一个与 x 轴的交点坐标,再利用交点式获得结果。两种方法各有千秋,仔细体会必定会有所收获。当然此题也可使用一般式,但不如这两种方法简单。 例 2、已知二次函数,当x=-1 时有最小值-4,且图像在x 轴上截得线段长为4,求函数解析式。 分析:当题目条件中点的条件不足三个时,要充分利用二次函数的对称性转化条件。在本题中由于所给条件能得到一个顶点坐标(-1,-4),另外一个条件是图像在x 轴上截得的线段长,条件似乎不是特别充分。仔细分析,有“当x=-1 时有最小值-4”就知道对称轴,再有“图像在 x 轴上截得线段长为 4”,利用对称性可得图像与 x 轴的交点坐标为(-3,0),(1,0),从而可利用交点式解决问题。 解: 当 x=-1 时有最小值-4,且图像在 x 轴上截得线段长为 4 ∴函数图像与 x 轴交于(-3,0),(1,0)两点。 ∴设二次函数的解析式为 二次函数过(-1,-4) ∴ ∴a=1 ∴ 点评:本题当然还可直接使用顶点坐标公式转化为关于 a,b,c 的两个等式,再利用“图像在 x 轴上截得线段长为 4”转化为,组合成一个关于 a,b,c 的方程组来解。不过这种方法计算量大一些。 例 3、如图,已知...