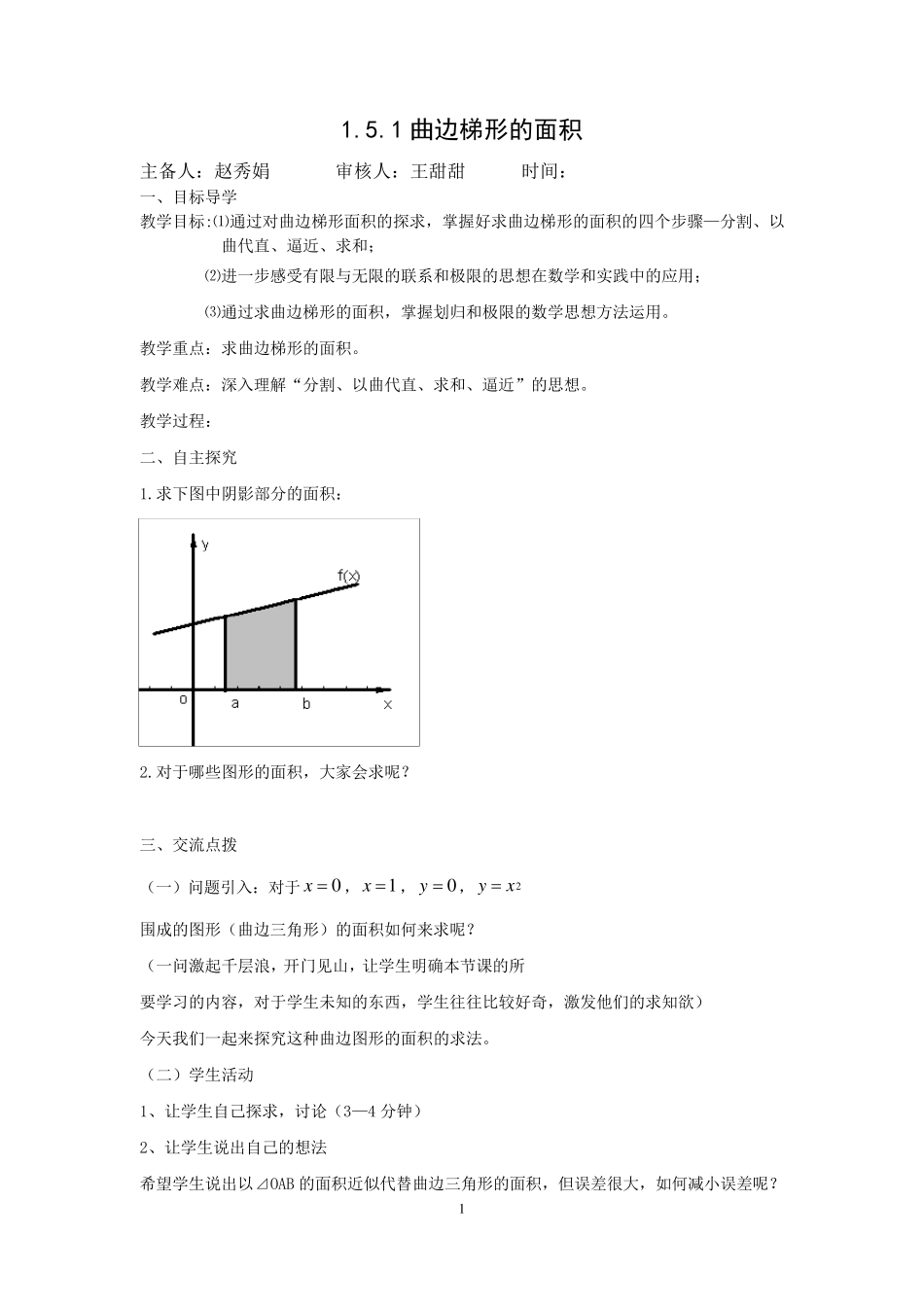
1 1.5.1 曲边梯形的面积 主备人:赵秀娟 审核人:王甜甜 时间: 一、目标导学 教学目标:⑴通过对曲边梯形面积的探求,掌握好求曲边梯形的面积的四个步骤—分割、以曲代直、逼近、求和; ⑵进一步感受有限与无限的联系和极限的思想在数学和实践中的应用; ⑶通过求曲边梯形的面积,掌握划归和极限的数学思想方法运用。 教学重点:求曲边梯形的面积。 教学难点:深入理解“分割、以曲代直、求和、逼近”的思想。 教学过程: 二、自主探究 1.求下图中阴影部分的面积: 2.对于哪些图形的面积,大家会求呢? 三、交流点拨 (一)问题引入:对于0x ,1x ,0y ,2yx围成的图形(曲边三角形)的面积如何来求呢? (一问激起千层浪,开门见山,让学生明确本节课的所要学习的内容,对于学生未知的东西,学生往往比较好奇,激发他们的求知欲) 今天我们一起来探究这种曲边图形的面积的求法。 (二)学生活动 1、让学生自己探求,讨 论 (3—4 分钟 ) 2、让学生说 出 自己的想法 希 望 学生说 出 以⊿ OAB 的面积近似 代替 曲边三角形的面积,但 误 差 很 大,如何减 小 误 差 呢?2 希望学生讨论得出将曲边三角形进行分割,形成若干个曲边梯形。(在讨论的过程中渗透分割的思想) 问题:如何计算每个曲边梯形的面积呢?(通过讨论希望学生能出以下三种方案,在讨论的过程中,让学生想到以直代曲,给学生创新的机会) 方案一 方案二 方案三 方案一:用一个矩形的面积近似代替曲边梯形的面积,梯形分割的越多,三角形的面积越小,小矩形的面积就可以近视代替曲边梯形的面积。 方案二:用一个大矩形的面积来近似代替曲边梯形的面积,梯形分割的越多,三角形的面积越小,大矩形的面积来近似代替曲边梯形的面积。 方案三:以梯形的面积来近似代替曲边梯形的面积。 (对于其中的任意一个曲边梯形,我们可以用“直边”来代替“曲边”(即在很小的范围内以直代曲),这三种方案是本节课内容的核心,故多花点时间引导学生探求,讨论得出,让学生体会“以曲代直”的思想,从近似中认识精确,给学生探求的机会) 总结:这样,我们就可以计算出任意一个小曲边梯形的面积的近似值,从而可以计算出整个曲边三角形面积的近似值,(求和),并且分割越细,面积的近似值就越精确,当分割无限变细时,这个近似值就无限逼近所求的曲边三角形的面积。如何求这个曲边三角形的面积,以方案一为例: ⑴分割细化...