正弦扫频信号幅值及相位的提取

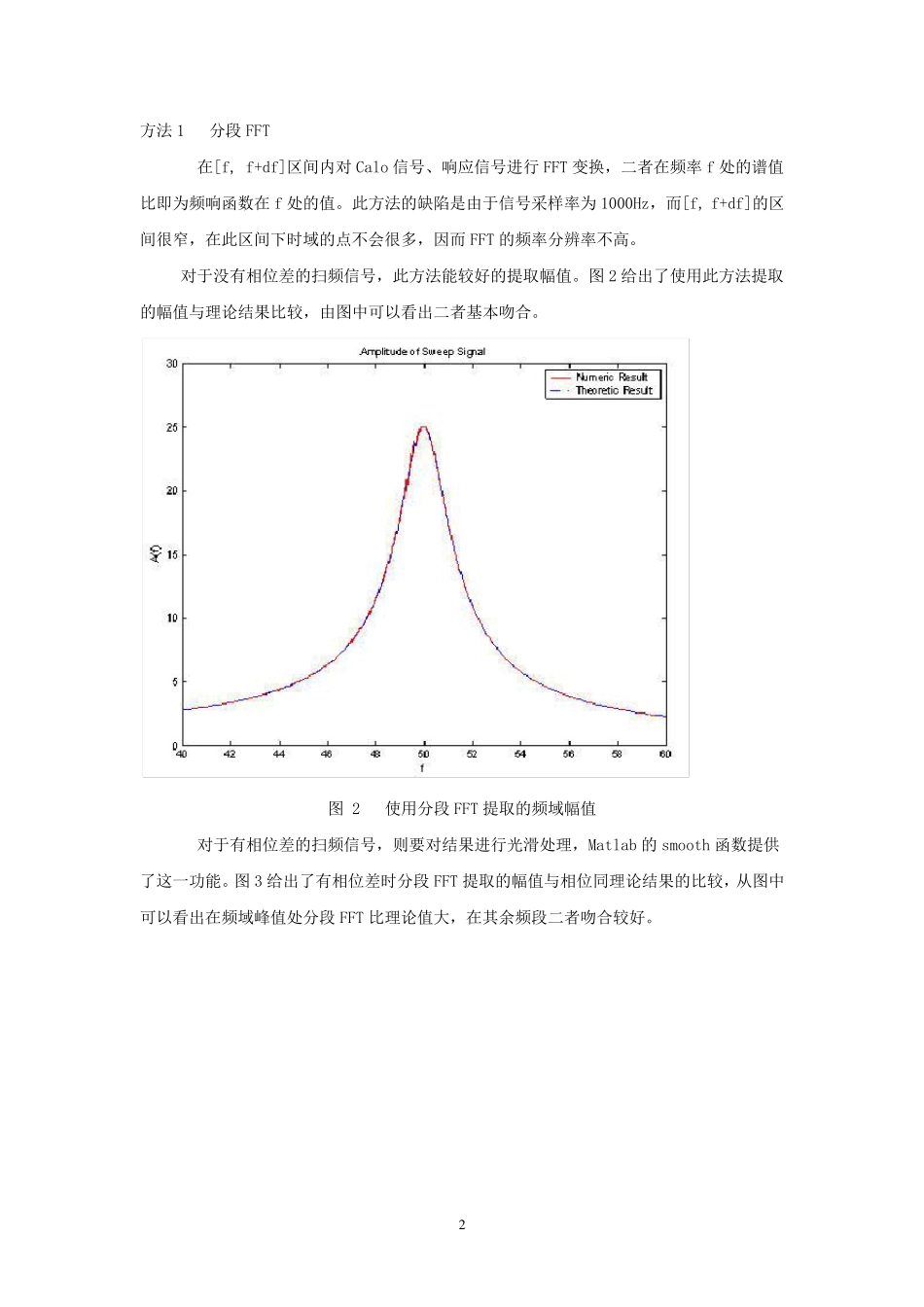
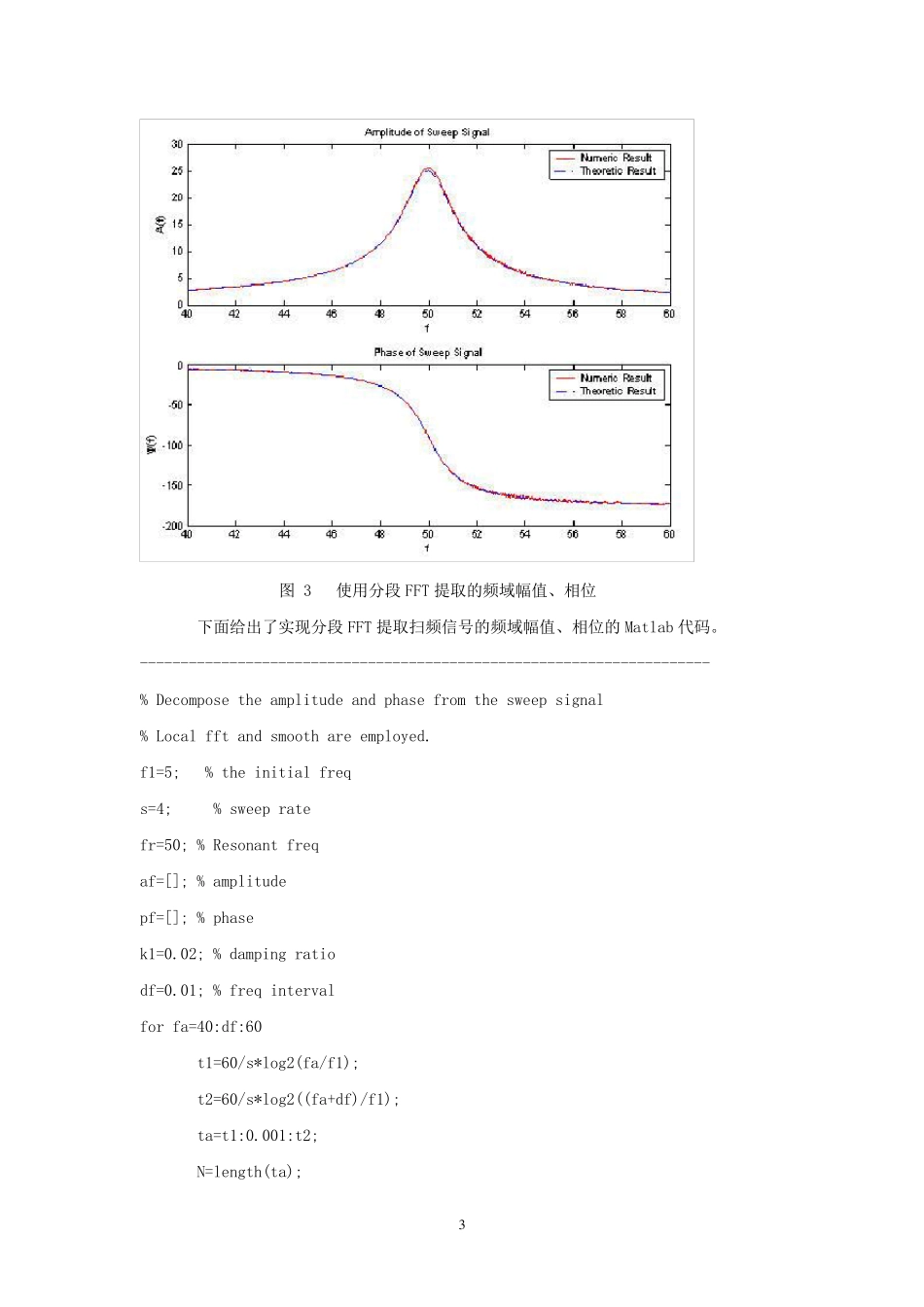
1 正弦扫频信号幅值及相位的提取(1) 正弦振动控制系统提供输入的扫频信号 ，对于对数扫频， ，其中Sr 为对数扫描率，若频响函数为 则系统输出为 。 测量系统中可得到 Calo 信号及响应信号，通过对二者进行数据处理，可得到频域下的响应 。不知道 LMS 的信号采集软件是如何提取频域响应的，个人认为软件计算速度有限，LMS 应该是通过硬件实现的。下面我提供几种方法并进行比较。 算例对于Calo 信号 ，频响函数为 ，其中 ，信号采样率为1000 次/秒，图 1 给出了时域下的响应信号。 图 1 时域下的响应信号 正弦扫频信号幅值及相位的提取(2) 2 方法1 分段FFT 在[f, f+df]区间内对Calo 信号、响应信号进行 FFT 变换，二者在频率 f 处的谱值比即为频响函数在f 处的值。此方法的缺陷是由于信号采样率为 1000Hz，而[f, f+df]的区间很窄，在此区间下时域的点不会很多，因而 FFT 的频率分辨率不高。 对于没有相位差的扫频信号，此方法能较好的提取幅值。图 2 给出了使用此方法提取的幅值与理论结果比较，由图中可以看出二者基本吻合。 图 2 使用分段FFT 提取的频域幅值 对于有相位差的扫频信号，则要对结果进行光滑处理，Matlab 的 smooth 函数提供了这一功能。图 3 给出了有相位差时分段FFT 提取的幅值与相位同理论结果的比较，从图中可以看出在频域峰值处分段FFT 比理论值大，在其余频段二者吻合较好。 3 图 3 使用分段FFT 提取的频域幅值、相位 下面给出了实现分段FFT 提取扫频信号的频域幅值、相位的Matlab 代码。 ---------------------------------------------------------------------- % Decompose the amplitude and phase from the sweep signal % Local fft and smooth are employed. f1=5; % the initial freq s=4; % sweep rate fr=50; % Resonant freq af=[]; % amplitude pf=[]; % phase k1=0.02; % damping ratio df=0.01; % freq interval for fa=40:df:60 t1=60/s*log2(fa/f1); t2=60/s*log2((fa+df)/f1); ta=t1:0.001:t2; N=length(ta); 4 ft=f1*2.^(s/60*ta); A1=sin(2*pi*ft.*ta); lamb=ft/fr; B1=1./(1-lamb.^2+j*2*k1*lamb); % transfer function A2=abs(B1).*sin(2*pi*ft.*ta+angle(B1)); ffreq=exp(-j*2*pi*(fa-400)*ta); % freq shift for time domain spa=fft(ffreq.*A1); spb=fft(ffre...