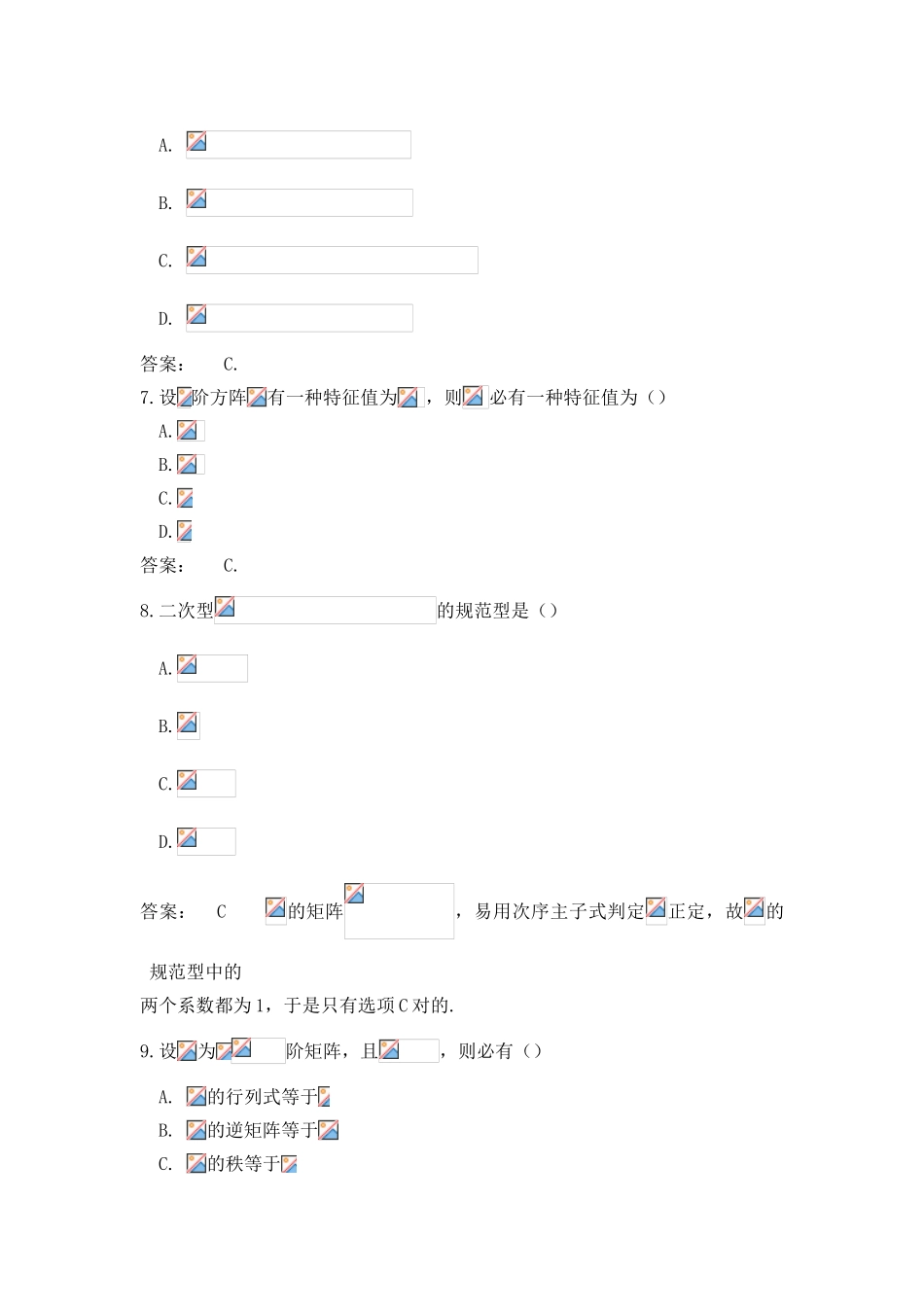
10 月全国自考《工程数学-线性代数》模拟试卷(一)一、单项选择题(本大题共 10 小题,每题 2 分,共 20 分)在每题列出的四个备选项中只有一种是符合题目规定的,请将其代码填写在题后的括号内。错选、多选或未选均无分。 1.设是矩阵, 是矩阵,假如乘积故意义,则应是() A.矩阵 B.矩阵 C.矩阵 D.矩阵 答案: D 2.若行列式() A. B. C. D.答案: B 3.设为阶方阵,那么有() A. B. C. D. 答案: B 4.设均为维向量,则下列结论中对的的是() A.若对任一组不全为零的数,均有,则线性无关 B.若线性有关,则对任意一组不全为零的数,都有 C.若,则线性有关 D.若向量组中任意两个向量都不成比例,则线性无关答案: A5.设向量组线性无关,则下列向量组中线性无关的是() A. B. C. D. 答案: B 由于,且矩阵为满秩矩阵,故线性无关.6.设元齐次线性方程组的一种基础解系为,则下列向量组中为的基础解系的是() A. B. C. D. 答案: C.7.设 阶方阵有一种特征值为,则必有一种特征值为() A. B. C. D. 答案: C.8.二次型的规范型是() A. B. C. D. 答案: C 的矩阵,易用次序主子式判定正定,故的规范型中的两个系数都为 1,于是只有选项 C 对的.9.设为阶矩阵,且,则必有() A. 的行列式等于 B. 的逆矩阵等于 C. 的秩等于 D. 的特征值均为 答案: C 10.已知矩阵与对角矩阵相似,则() A. B. C. D. 答案: C 由于与对角矩阵相似,从而存在可逆阵,使,二、填空题(本大题共 10 小题,每题 2 分,共 20 分)请在每题的空格中填上对的答案。错填、不填均无分。11.若,则 . 答案:12.若方程组有非零解,则常数 .答案:13.设则 .答案: 14.已知为矩阵的 2 重特征值,则的另一种特征值为 .答案: 解析: 由于 , 故15.齐次线性方程组的基础解系中所含向量个数为 .答案:216.设矩阵但其中则矩阵的秩 . 答案:1 解析:因因此的两个列向量都是齐次线性方程组的解,而的两个列向量是线性无关的,故的基础解系中至少含 2 个向量,而基础解系中所含向量个数为因此即此外故17.设 2 阶矩阵,则 .答案:618.设则 .答案:19.若矩阵,则二次型 .答案:20.已知 2 阶方阵的特征值为则 .答案:36 解析:由特征值的性质知的所有特征值为 4,9,故.三、计算题(本大题共 6 小题,每题 9 分,共 54 分)21.计算行列式解:.22.已知矩阵矩阵...