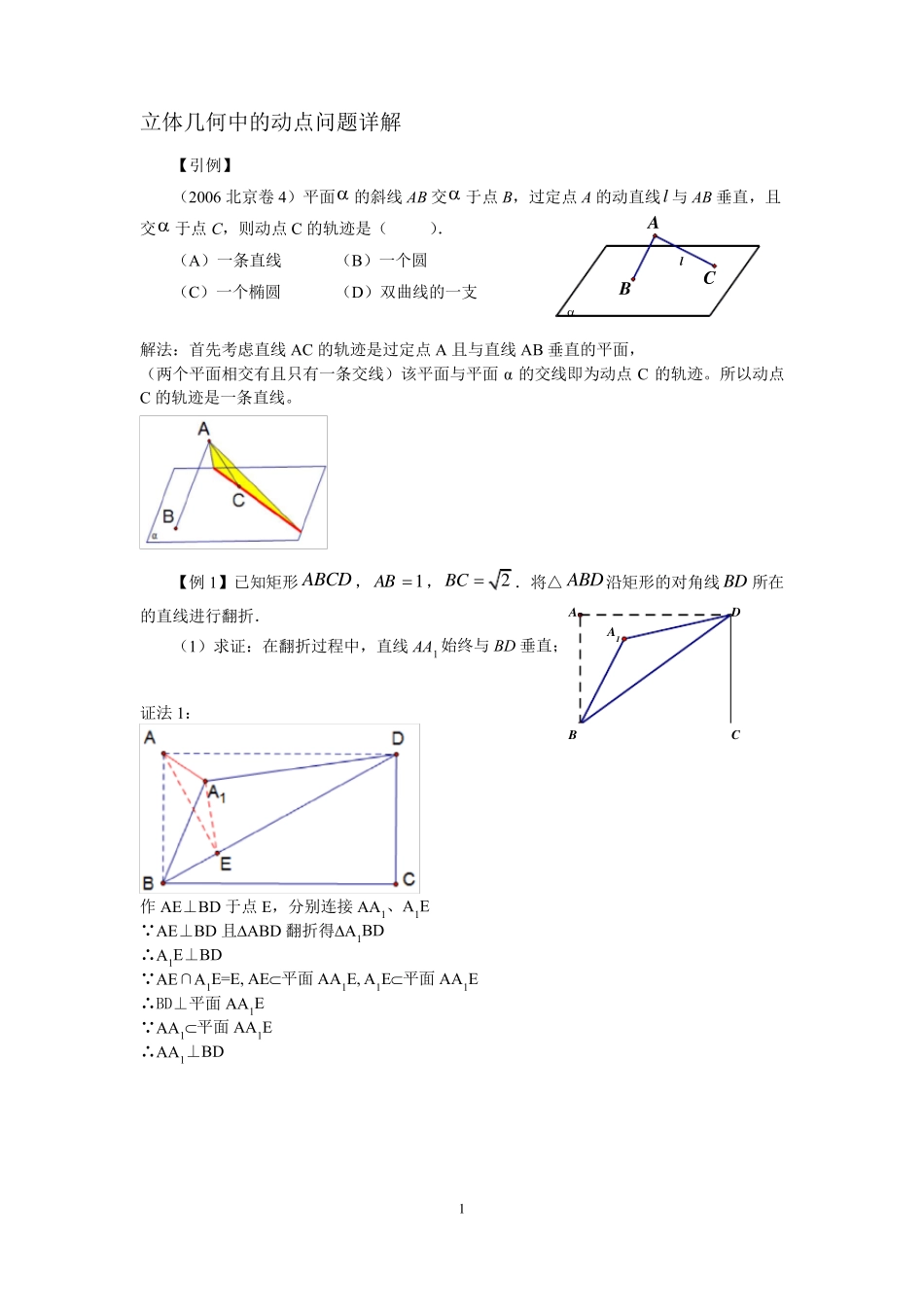
1 laBACDABCA1立体几何中的动点问题详解 【引例】 (2006 北京卷4)平面a 的斜线AB 交a 于点B,过定点A 的动直线l与AB 垂直,且交a 于点C,则动点C 的轨迹是( ). (A)一条直线 (B)一个圆 (C)一个椭圆 (D)双曲线的一支 解法:首先考虑直线AC 的轨迹是过定点A 且与直线AB 垂直的平面, (两个平面相交有且只有一条交线)该平面与平面α 的交线即为动点C 的轨迹。所以动点C 的轨迹是一条直线。 【例1】已知矩形ABCD ,1AB , 2BC .将△ABD沿矩形的对角线BD 所在的直线进行翻折. (1)求证:在翻折过程中,直线AA1 始终与BD 垂直; 证法1: 作AE⊥BD 于点E,分别连接AA1、A1E AE⊥BD 且ABD 翻折得A1BD ∴A1E⊥BD AE∩A1E=E, AE平面AA1E, A1E平面AA1E ∴BD⊥平面AA1E AA1平面AA1E ∴AA1⊥BD 2 DABCA1 证法2: 连接AA1,取AA1 的中点E,分别连接BE、DE ABD 翻折得A1BD ∴BA=BA1,DA=DA1 点E 是 AA1 的中点 ∴AA1⊥BE, AA1⊥DE BE∩ DE=E, BE平面 BDE, DE平面 BDE ∴AA1⊥平面 BDE BD平面 BDE ∴AA1⊥BD (2)在翻折过程中,以下说法正确的是____________. ① 存在某个位置,使得直线1A C 与直线 BD 垂直. ② 存在某个位置,使得直线1A B 与直线CD 垂直. ③ 存在某个位置,使得直线1A D 与直线 BC 垂直. 解法1:(运动轨迹) 点A1 的轨迹在直线 BD 的垂面 A1AF 上,而点C 在直线 BD 的垂面 HGC 上 垂面 A1AF//垂面 HGC 所以点A1 不在平面 HGC 上 由于过点C 且垂直于 BD 的直线都在平面 HGC 上 所以①不成立 由于 A1 的轨迹可以落在过点B 的直线 CD 的垂面上,所以②成立 又由于 A1 的轨迹无法落在过点D 的直线 BC 的垂面上,所以③不成立 3 解法2;(借助三垂线定理平面化垂直关系) 借助三垂线定理解决(借助正投影把空间垂直转化到平面上解决) 点A1 在平面ABCD 上的正投影为点H,而H 的轨迹为线段AA’ 由于BH 与BD 不可能垂直,所以直线1A C 与直线垂直BD 是不可能的,因此①不成立 由于点H 落在BC 上时刚好BH 与CD 垂直,所以②成立 由于HD 与BC 不可能垂直,所以直线1A D 与直线垂直BC 是不可能的,因此③不成立 解法:3(假设----检验) 假设直线1A C 与直线BD 垂直,由于A1E⊥BD 易证得 BD⊥平面A1CE 所以BD⊥CE(矛盾)...