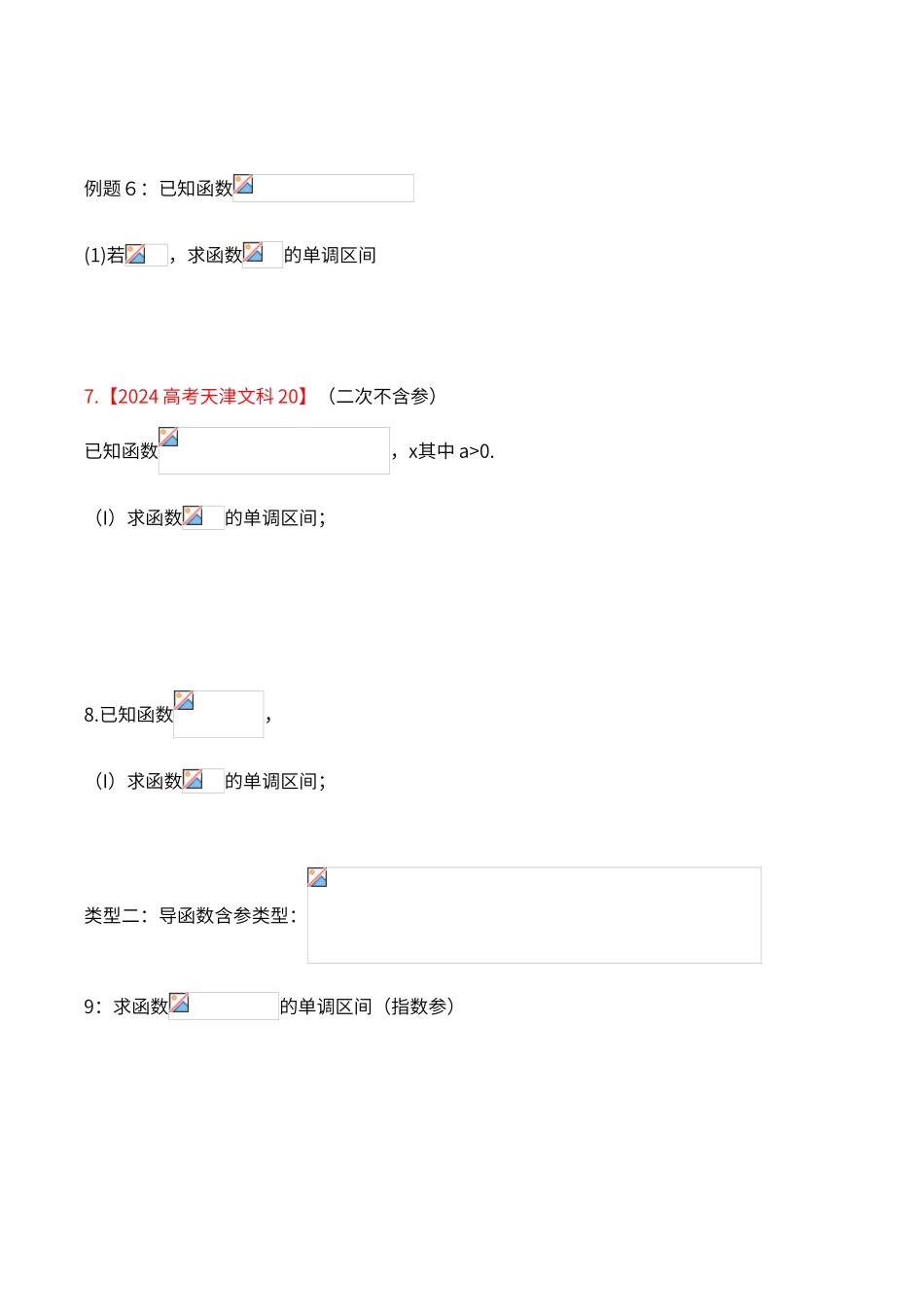
类型二:导数单调性专题类型1.导数不含参。类型2.导数含参。类型3:要求二次导求单调性一般步骤:(1) 第一步:写出定义域,一般有(2)第二步:求导,(注意有常数的求导)若有分母则通分。一般分母都比 0 大,故去死 若无分母,因式分解(提公因式,十字相乘法)或求根(观察分子)推断导函数是否含参,再进行讨论(按恒成立与两个由为分界)(3)第三步由 (4)下结论类型一:导函数不含参:对于这类型的题,直接由导函数大于 0,小于 0 即可(除非恒成立)例题1求函数的单调递增区间解:由所以函数在区间单调递增 由所以函数在区间单调递减 例题2:求函数的单调区间解:由所以函数在区间单调递增 由所以函数在区间单调递减 例题3:求函数的单调区间例题4:已知函数(1)若时,求函数的单调区间例题5.(2024·新课标全国文,21)设函数 f(x)=x(ex-1)-ax2.(1)若 a=,求 f(x)的单调区间;例题6:已知函数(1)若,求函数的单调区间7.【2024 高考天津文科 20】(二次不含参)已知函数,x其中 a>0.(I)求函数的单调区间;8.已知函数,(I)求函数的单调区间;类型二:导函数含参类型:9:求函数的单调区间(指数参)例题 10.(2024 北京理)(一次参)设函数(Ⅰ)求曲线在点处的切线方程;(Ⅱ)求函数的单调区间;例题 11.(二次参)设函数,其中常数(Ⅰ)讨论的单调性;(Ⅱ)若当 x≥0 时,f(x)>0 恒成立,求 a 的取值范围。例题 12:求函数上的单调区间例题 13.(2024 安徽卷理)( 二次参) 已知函数,讨论的单调性.14.(2024 辽宁卷理)(本小题满分 12 分)已知函数,其中,讨论函数的单调性。15.(2024 陕西卷文)(本小题满分 12 分)已知函数求的单调区间; 16.【2024 高考新课标文 21】(本小题满分 12 分)设函数 f(x)= ex-ax-2(Ⅰ)求 f(x)的单调区间17.【2024 高考全国文 21】已知函数(Ⅰ)讨论的单调性;18.【2024 高考全国文 21】已知函数.(1)设是的极值点.求 ,并求的单调区间;训练:(1)求函数 的单调区间。训练:(2)求函数 的单调区间。训练:(3)求函数 的单调区间训练:(4)求函数 的单调区间训练:(5)求函数 的单调区间近3年全国高考导数试题1.(2024 全国卷3)已知函数 (1) 若,求的值2.(2024 全国卷2)已知函数 ,且(1)求的值3.(2024 全国卷1)已知函数 ,(1)讨论的单调性4(2024 全国卷 2)已知函数 的单调性,证明:在上单调递减,在上单调递...