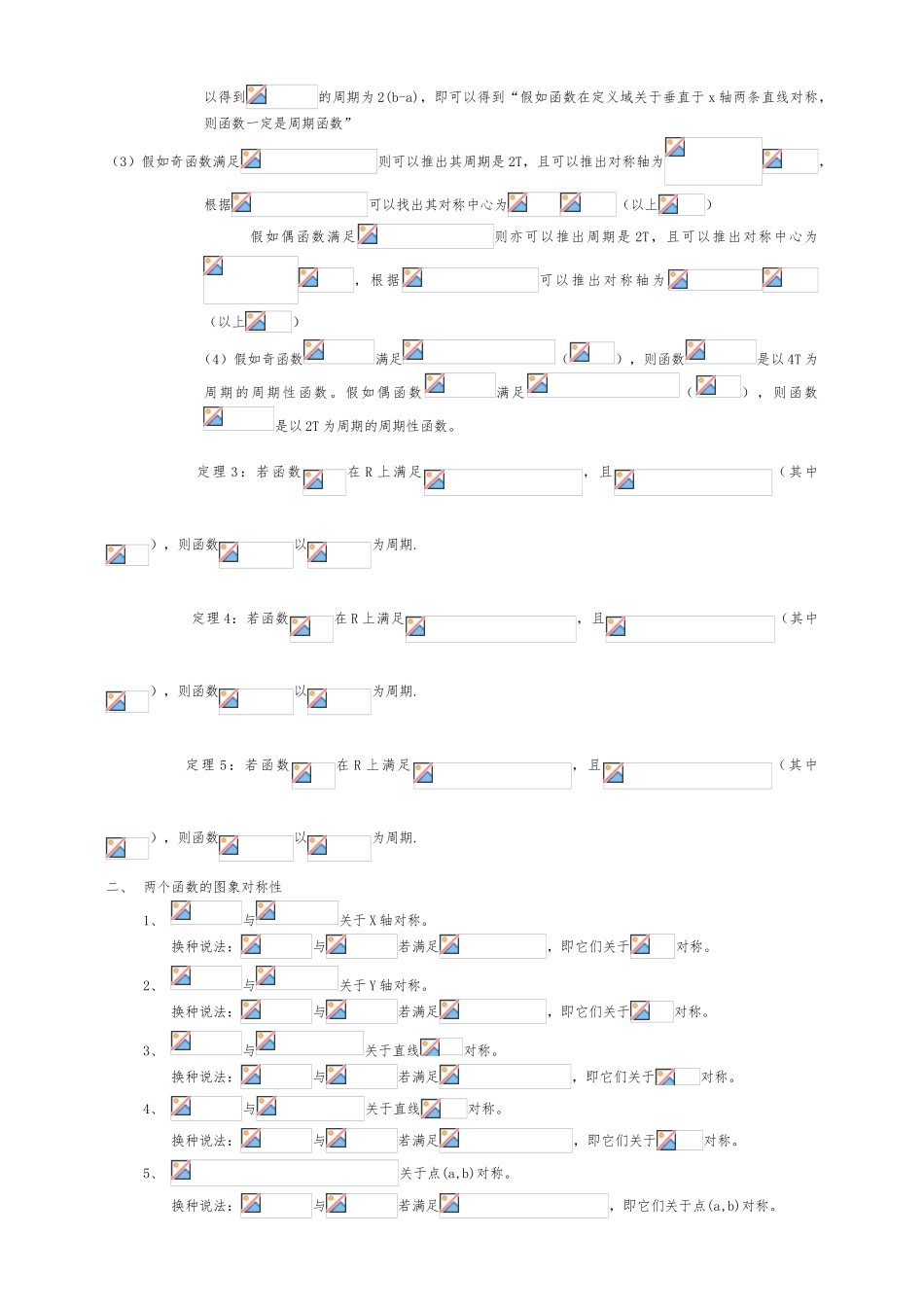
函数的对称性和奇偶性函数 函数对称性、周期性基本知识一、 同一函数的周期性、对称性问题(即函数自身)1、 周期性:对于函数,假如存在一个不为零的常数 T,使得当 x 取定义域的每一个值时,都有都成立,那么就把函数叫做周期函数,不为零的常数 T 叫做这个函数的周期。假如所有的周期中存在着一个最小的正数,就把这个最小的正数叫做最小正周期。2、 对称性定义(略),请用图形来理解。3、 对称性:我们知道:偶函数关于 y(即 x=0)轴对称,偶函数有关系式 奇函数关于(0,0)对称,奇函数有关系式上述关系式是否可以进行拓展?答案是肯定的 探讨:(1)函数关于对称、、 ( 异号考虑对称 ) 也可以写成或简 证 : 设 点在上 , 通 过可 知 ,, 即 点上,而点与点关于 x=a 对称。得证。若写成:,函数关于直线对称(2)函数关于点对称或简 证 : 设 点在上 , 即, 通 过可 知 ,,所以,所以点也在上,而点与关于对称。得证。若写成:,函数关于点对称(3)函数关于点对称:假设函数关于对称,即关于任一个值,都有两个 y 值与其对应,显然这不符合函数的定义,故函数自身不可能关于对称。但在曲线 c(x,y)=0,则有可能会出现关于对称,比如圆它会关于 y=0 对称。4、 周期性:(1)函数满足如下关系系,则 A、 B、 C、或(等式右边加负号亦成立) D、其他情形(2)函数满足且,则可推出即可以得到的周期为 2(b-a),即可以得到“假如函数在定义域关于垂直于 x 轴两条直线对称,则函数一定是周期函数”(3)假如奇函数满足则可以推出其周期是 2T,且可以推出对称轴为,根据可以找出其对称中心为(以上) 假如偶函数满足则亦可以推出周期是 2T,且可以推出对称中心为,根据可以推出对称轴为(以上) (4)假如奇函数满足(),则函数是以 4T 为周期的周期性函数。假如偶函数满足(),则函数是以 2T 为周期的周期性函数。定理 3:若函数在 R 上满足,且(其中),则函数以为周期. 定理 4:若函数在 R 上满足,且(其中),则函数以为周期. 定理 5:若函数在 R 上满足,且(其中),则函数以为周期.二、 两个函数的图象对称性1、与关于 X 轴对称。换种说法:与若满足,即它们关于对称。2、与关于 Y 轴对称。换种说法:与若满足,即它们关于对称。3、与关于直线对称。换种说法:与若满足,即它们关于对称。4、与关于直线对称。换种说法:与若满足,即它们关于对称。5、...