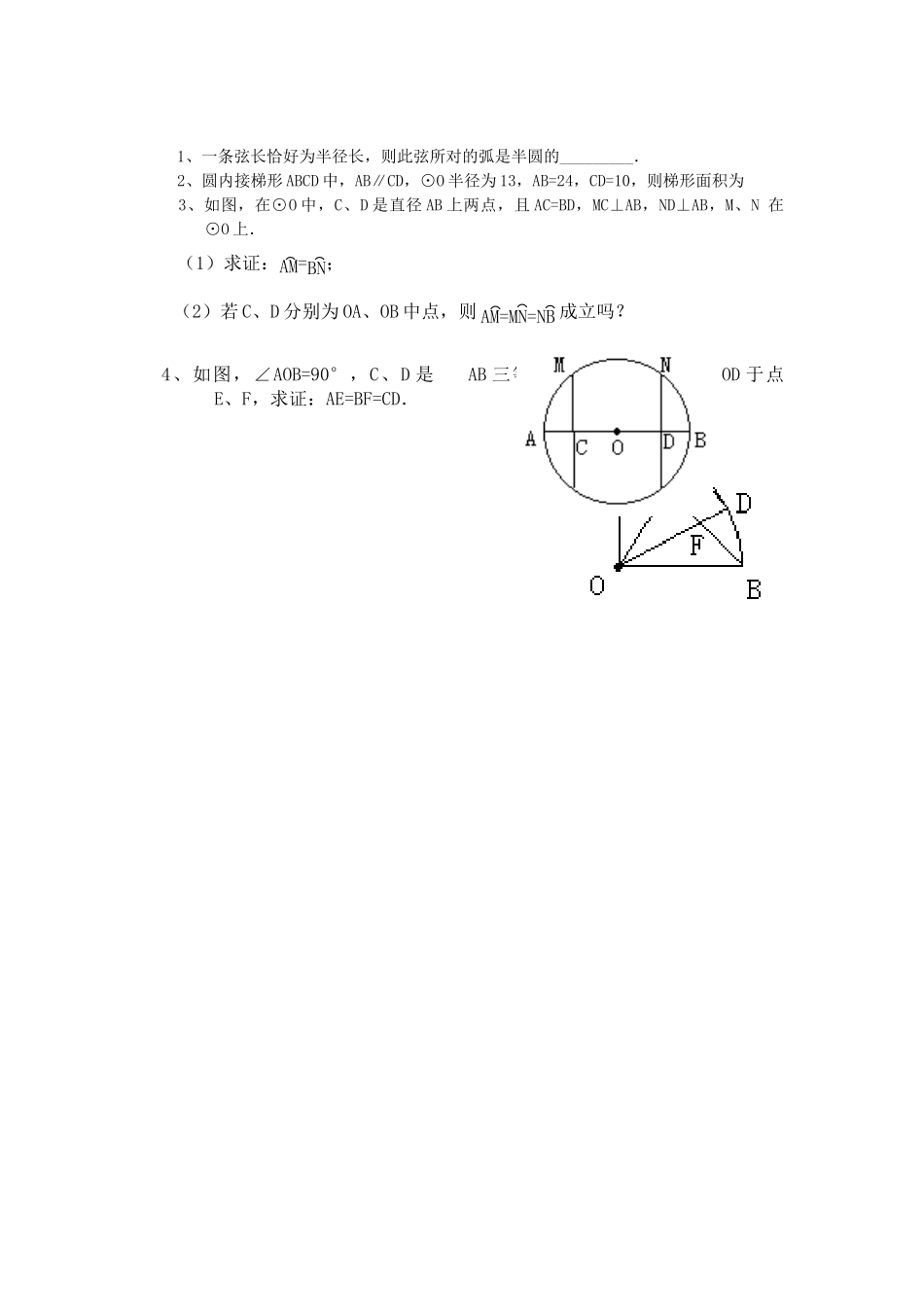
BAOB'BAA'O《圆》第一节 弧、弦、圆心角导学案 1主编人: 主审人:班级: 学号: 姓名: 学习目标:【知识与技能】1 理解圆的旋转不变性,掌握圆心角的概念以及弧、弦、圆心角之间的相等关系,并能运用这些关系解决有关的证明、计算2 弧、弦、圆心角之间的相等关系是论证同圆或等圆中弧相等、角相等、线段相等的主要依据【过程与方法】经历探究发现圆的旋转不变性,证明圆心角、弦、弧之间的关系【情感、态度与价值观】学生通在探究圆的旋转不变性,圆心角、弧、弦之间关系过程中体验其成立的喜悦【重点】弧、弦、圆心角之间的相等关系【难点】定理的证明学习过程:一、自主学习(一)复习巩固(1)圆是轴 图形,任何一条 所在直线都是它的对称轴. (2)垂径定理 推论 .(二)自主探究如图所示,∠AOB 的顶点在圆心,像这样顶点在圆心的角叫做 . 请同学们按下列要求作图并回答问题:如图所示的⊙O 中,分别作相等的圆心角∠AOB和∠A′OB′将圆心角∠AOB 绕圆心O 旋转到∠A′OB′的位置,你能发现哪些等量关系?为什么?相等的弦: ;相等的弧: 理由: 结论:在同圆或等圆中,相等的圆心角所对的 相等,所对的弦也 . 表达式: 同样,还可以得到:在同圆或等圆中,假如两条弧相等,那么它们所对的 相等,所对的弦也 .表达式: 在同圆或等圆中,假如两条弦相等,那么它们所对的圆心角 ,所对的 也相等.表达式: 注:同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也 。(三)、归纳总结: 在同圆或等圆中,相等的圆心角所对的 相等,所对的弦也 .在同圆或等圆中,假如两条弧相等,那么它们所对的 相等,所对的弦也 ⌒OBACEDF⌒⌒ ⌒⌒⌒⌒⌒⌒⌒⌒⌒⌒⌒.在同圆或等圆中,假如两条弦相等,那么它们所对的圆心角 ,所对的 也相等.(四)自我尝试:1、如图,在⊙O 中,AB=AC ∠ACB =60 °,求证∠AOB=∠BOC=∠AOC2、如图,AB,CD 是⊙O 的两条弦。(1)假如 AB=CD,那么 , (2)假如 AB=CD,那么 , (3)假如∠AOB=∠COD,那么 , (4)假如 AB=CD,OE⊥AB 于点 E,OF⊥CD 于点 F,OE 与 OF 相等吗?为什么?3、如图,AB 是⊙O 的直径,BC=CD=DE,∠COD=35 °,求∠AOE 的度数。二、老师点拔1、根据圆的旋转不变性,可以得出关于圆心角、弧、弦之间的关系:在同圆或等圆中,相等的圆心角所对的弧相等,反过来也成立,也就是说:在同...