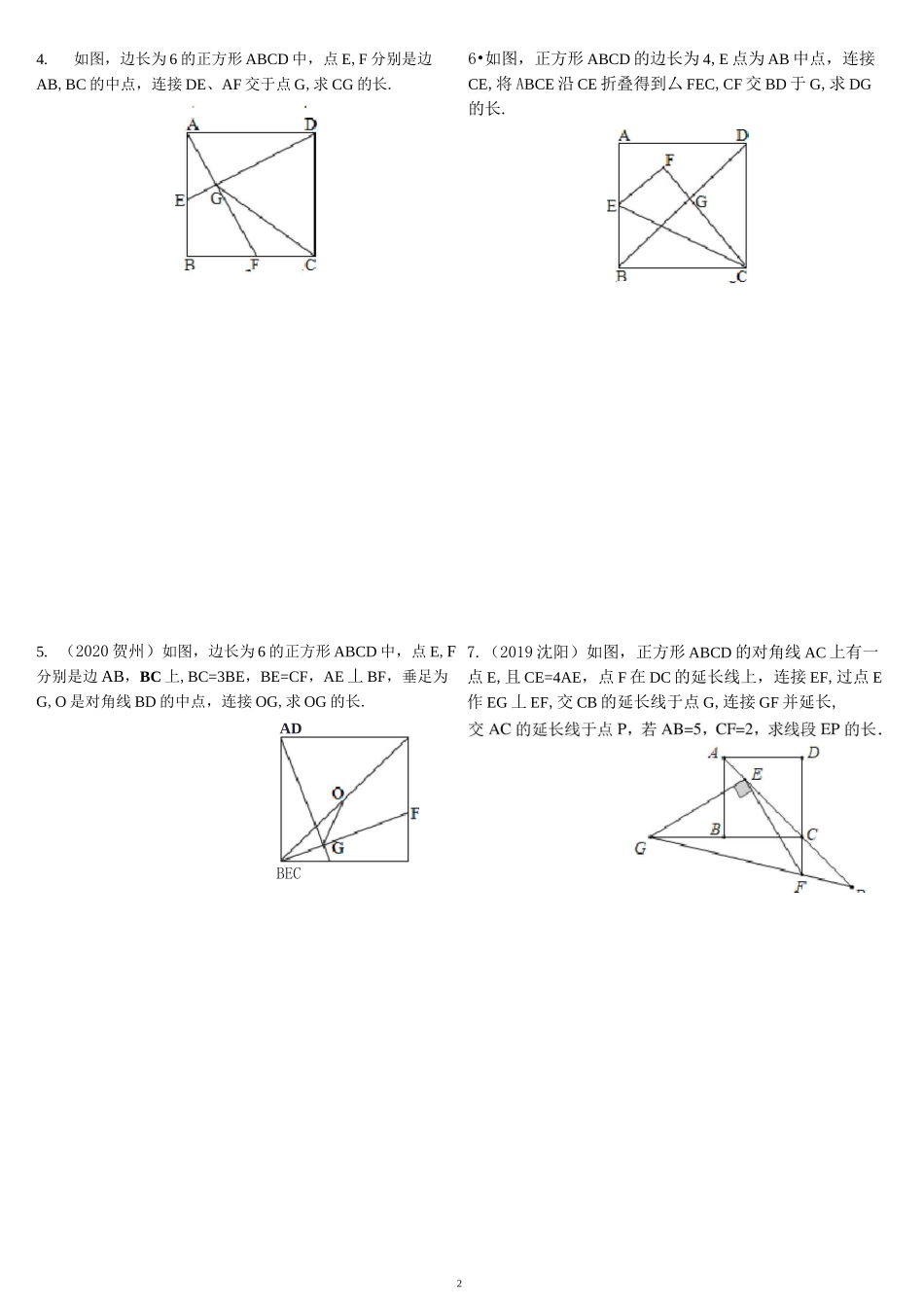
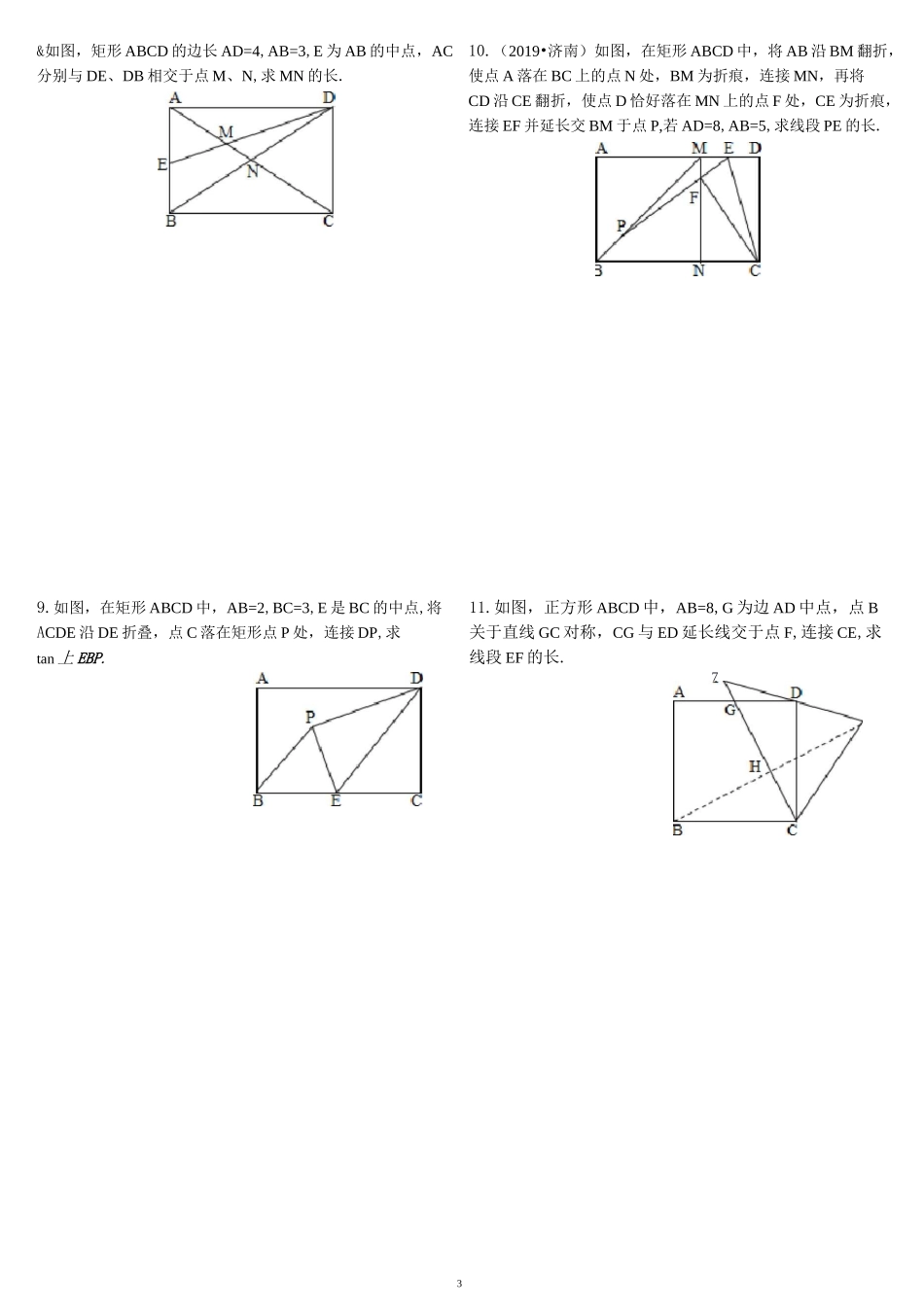
1建立直角坐标系解决几何问题【专题说明】在平面直角坐标系 xOy 中,我们知道线段 AB 的长取决于两个端点的坐标.2.如图,RtAABC 中,ZACB=90°,AC=3,BC=5,以 AB 为边向外作正方形 ABEF,求正方形中心 O 与点 C 的连线长.1.如图,在等边厶 ABC 中,BD=4,CE=2,连接 DE,M、N 分别为线段 DE、BC 的中点,求线段 MN 的长.3.(2020 郑州)如图,在边长为 2<2 的正方形 ABCD 中,点 E,F 分别是边 AB,BC 的中点,连接 EC,FD,点 G,H 分别是 EC,FD 的中点,F丿临 JibE在图 1 中,在图 2 中,在图 3 中,线段 AB//y 轴,则 AB 二 Iy—yI=y—y1212线段 AB//y 轴,则 AB 二 Ix—xI=x—x1212一般情况下,已知点 A(x,x),B(y,y),(y>y)12(x>x)121212若 x 丰 x 且 y 工 y,1212i 己作 AB2=(x 一 x)2+(y 一 y)2.1212图 1 到图 3 的三种情况,是坐标系里由两点坐标得到线段长的具体途径,这其实是一个由“数”到“形”的过程,是我们破解压轴题应该具备的技能.则 AB=〒(x-x)2+(y-y)2,有时候回121224.如图,边长为 6 的正方形 ABCD 中,点 E,F 分别是边AB,BC 的中点,连接 DE、AF 交于点 G,求 CG 的长.6•如图,正方形 ABCD 的边长为 4,E 点为 AB 中点,连接CE,将 ABCE 沿 CE 折叠得到厶 FEC,CF 交 BD 于 G,求 DG的长.5. (2020 贺州)如图,边长为 6 的正方形 ABCD 中,点 E,F分别是边 AB,BC 上,BC=3BE,BE=CF,AE 丄 BF,垂足为G,O 是对角线 BD 的中点,连接 OG,求 OG 的长.ADBEC7.(2019 沈阳)如图,正方形 ABCD 的对角线 AC 上有一点 E,且 CE=4AE,点 F 在 DC 的延长线上,连接 EF,过点 E作 EG 丄 EF,交 CB 的延长线于点 G,连接 GF 并延长,3&如图,矩形 ABCD 的边长 AD=4,AB=3,E 为 AB 的中点,AC分别与 DE、DB 相交于点 M、N,求 MN 的长.10.(2019•济南)如图,在矩形 ABCD 中,将 AB 沿 BM 翻折,使点 A 落在 BC 上的点 N 处,BM 为折痕,连接 MN,再将CD 沿 CE 翻折,使点 D 恰好落在 MN 上的点 F 处,CE 为折痕,连接 EF 并延长交 BM 于点 P,若 AD=8,AB=5,求线段 PE 的长.9.如图,在矩形 ABCD 中,AB=2,BC=3,E 是 BC 的中点,将ACDE 沿 DE 折叠,点 C 落在矩形点 P 处,连接 DP,求tan 上 EBP.11.如图,正方形 ABCD 中,AB=8,G 为边 AD ...