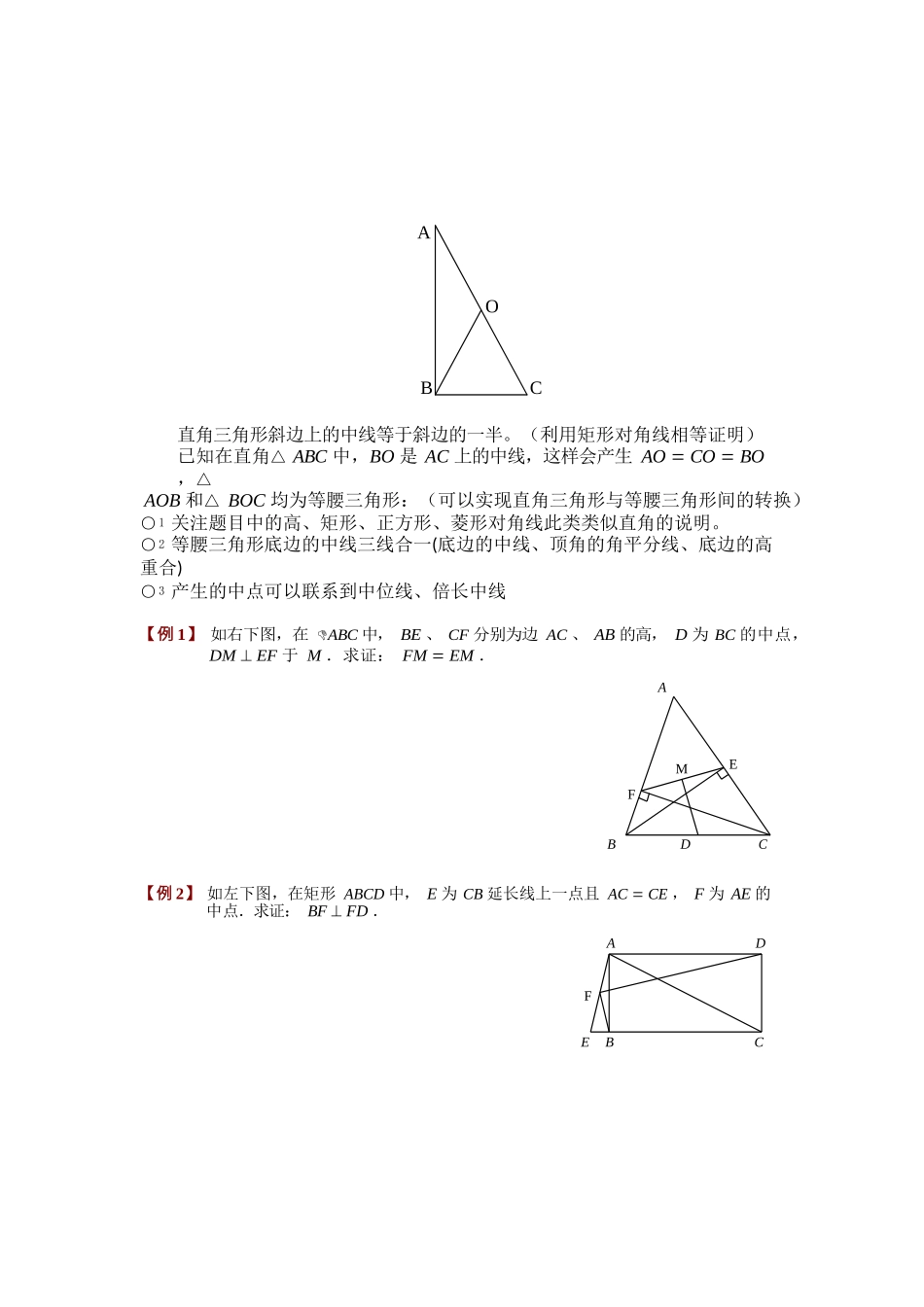
OMEFFABC直角三角形斜边上的中线等于斜边的一半。(利用矩形对角线相等证明) 已知在直角△ ABC 中,BO 是 AC 上的中线,这样会产生 AO CO BO ,△AOB 和△ BOC 均为等腰三角形:(可以实现直角三角形与等腰三角形间的转换)○1 关注题目中的高、矩形、正方形、菱形对角线此类类似直角的说明。○2 等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合)○3 产生的中点可以联系到中位线、倍长中线【例 1】 如右下图,在 ABC 中, BE 、 CF 分别为边 AC 、 AB 的高, D 为 BC 的中点,DM EF 于 M .求证: FM EM .ABDC【例 2】 如左下图,在矩形 ABCD 中, E 为 CB 延长线上一点且 AC CE , F 为 AE 的中点.求证: BF FD .ADEBCD【例 3】 在△ABC 中,CD 、AE 分别为 AB 、BC 边上的高,∠B 60 ,求证:DE 1 AC .2ABEC【例 4】 如图所示, P 是 ABC 内的一点, PAC PBC,过 P 作 PM AC 于 M ,PL BC 于 L , D 为 AB 的中点,求证 DM DL .