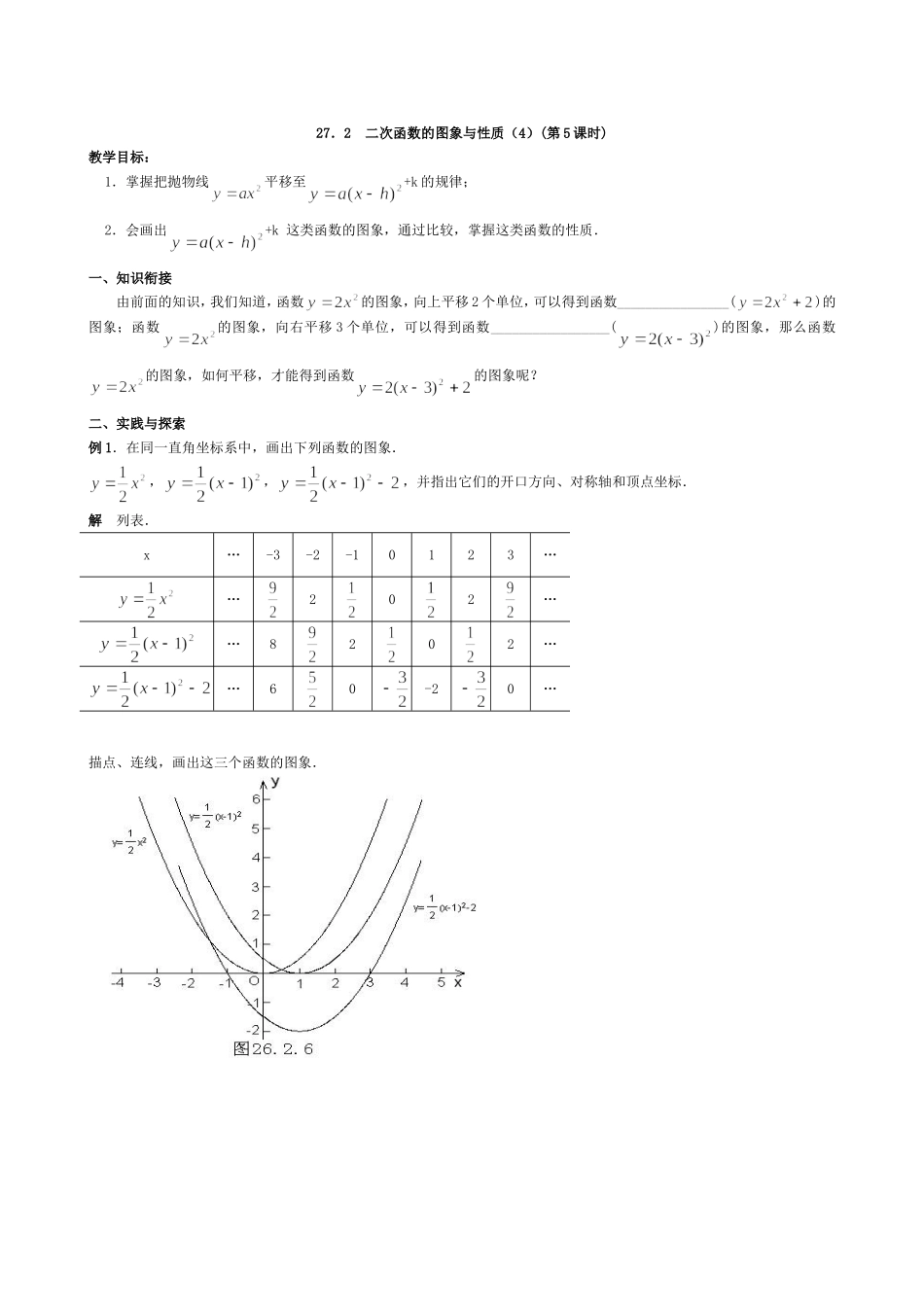
27.2 二次函数的图象与性质(4)(第 5 课时)教学目标:1.掌握把抛物线平移至+k 的规律;2.会画出+k 这类函数的图象,通过比较,掌握这类函数的性质.一、知识衔接由前面的知识,我们知道,函数的图象,向上平移 2 个单位,可以得到函数________________()的图象;函数的图象,向右平移 3 个单位,可以得到函数_________________()的图象,那么函数的图象,如何平移,才能得到函数的图象呢?二、实践与探索例 1.在同一直角坐标系中,画出下列函数的图象.,,,并指出它们的开口方向、对称轴和顶点坐标.解 列表.描点、连线,画出这三个函数的图象.x…-3-2-10123……202……8202……60-20…它们的开口方向都向 ,对称轴分别为 、 、 ,顶点坐标分别为 、 、 .并观察三个图象之间的关系.,把函数 y=的图象沿 x 轴向 平移 个单位长度,可得的图象;再把函数的图象沿 y 轴方向向 平移 个单位长度就可以得到函数的图象.即.把抛物线 y=-x2向_______平移______个单位,再向_______平移_______个单位,就得到抛物线 y=-(x+1)2-1.三、归纳1. 二次函数的图象的上下平移,只影响二次函数+k 中______________________的值;左右平移,只影响__________________________的值,抛物线的____ _________________不变,所以平移时,可根据 ______________ 的改变,确定平移前、后的函数关系式及平移的路径. 2、理一理知识点y=ax2y=ax2+ky=a (x-h)2y=a (x-h)2+k开口方向顶点对称轴最值增减性(对称轴右侧)3.抛物线 y=a (x-h)2+k 与 y=ax2形状___________,位置________________.例 2.把抛物线向上平移 2 个单位,再向左平移 4 个单位,得到抛物线,求 b、c 的值.四、课堂练习 1.y=3x2y=-x2+1y=(x+2)2y=-4 (x-5)2-3开口方向顶点对称轴最值增减性(对称轴左侧)2.y=6x2+3 与 y=6 (x-1)2+10_____________相同,而____________不同.3.顶点坐标为(-2,3),开口方向和大小与抛物线 y=x2相同的解析式为( ) A.y=(x-2)2+3B.y=(x+2)2-3 C.y=(x+2)2+3D.y=-(x+2)2+34.二次函数 y=(x-1)2+2 的最小值为__________________.5.将抛物线 y=5(x-1)2+3 先向左平移 2 个单位,再向下平移 4 个单位后,得到抛物线的解析式为_______________________.6.若抛物线 y=ax2+k 的顶点在直线 y=-2 上,且 x=1 时,y=-3,求 a...