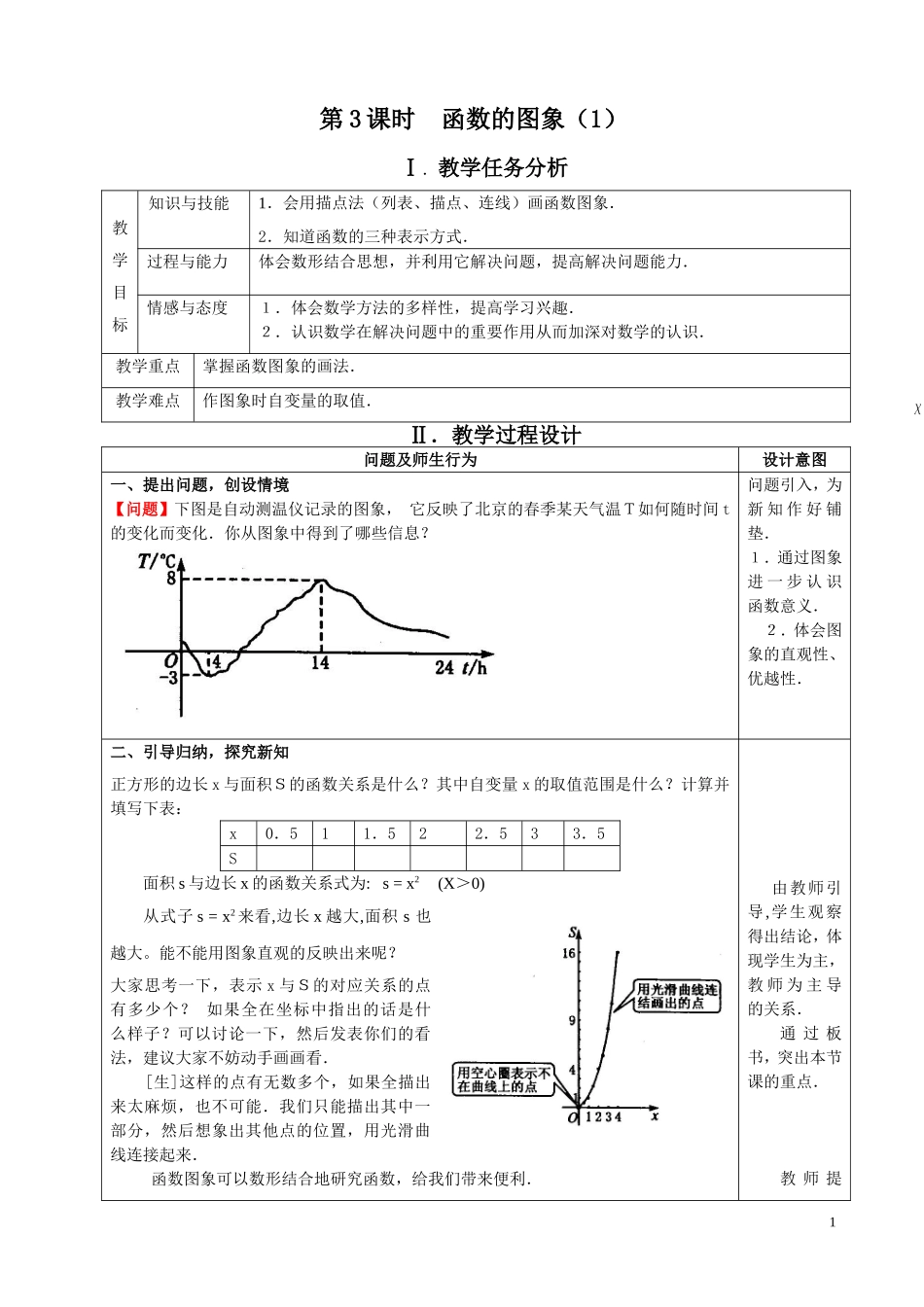
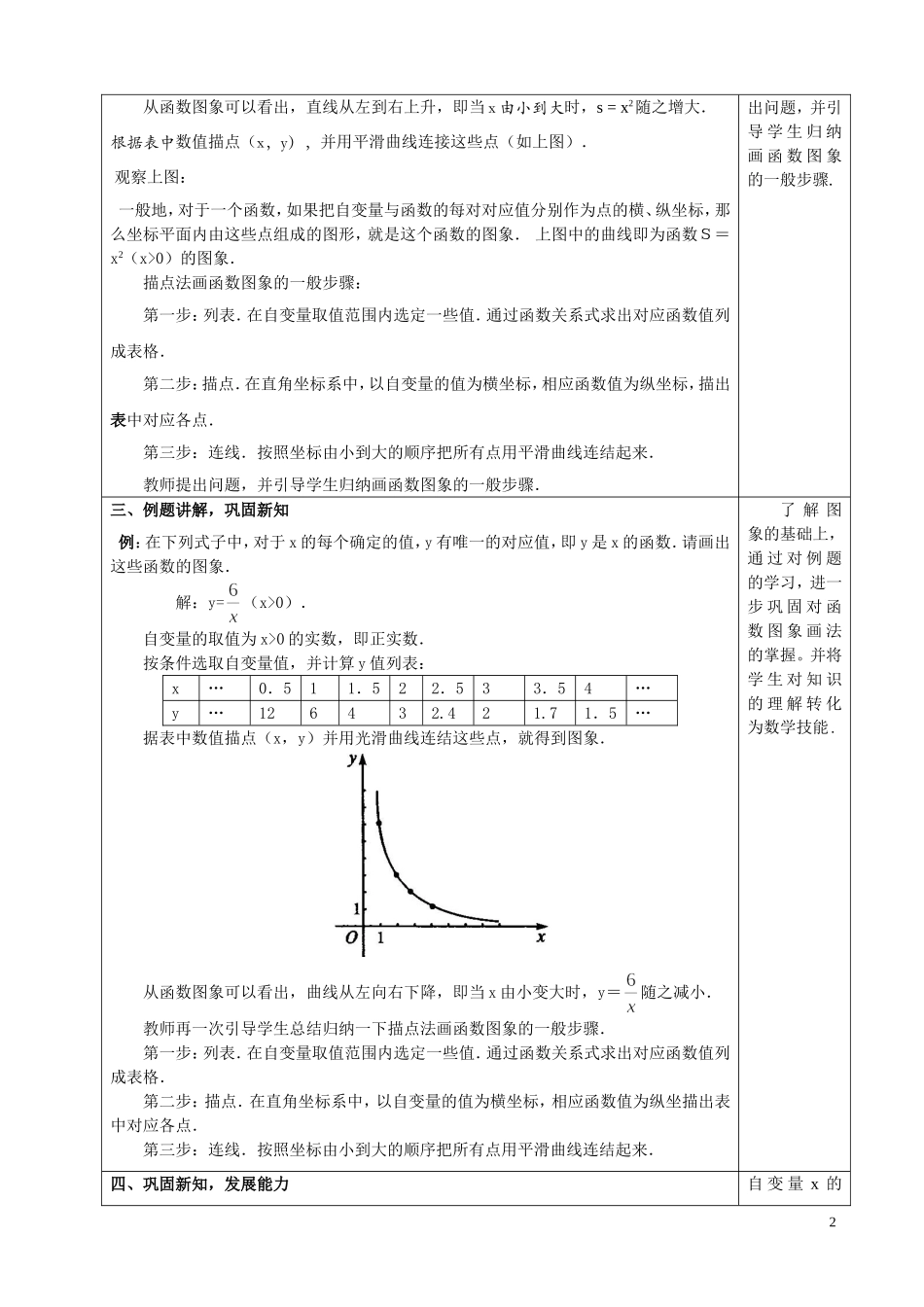
第 3 课时 函数的图象(1) Ⅰ.教学任务分析 教学目标知识与技能1.会用描点法(列表、描点、连线)画函数图象.2.知道函数的三种表示方式.过程与能力体会数形结合思想,并利用它解决问题,提高解决问题能力.情感与态度1.体会数学方法的多样性,提高学习兴趣.2.认识数学在解决问题中的重要作用从而加深对数学的认识.教学重点掌握函数图象的画法.教学难点作图象时自变量的取值.Ⅱ.教学过程设计问题及师生行为设计意图一、提出问题,创设情境【问题】下图是自动测温仪记录的图象,它反映了北京的春季某天气温T如何随时间 t的变化而变化.你从图象中得到了哪些信息?问题引入,为新 知 作 好 铺垫.1.通过图象进 一 步 认 识函数意义. 2.体会图象的直观性、优越性.二、引导归纳,探究新知正方形的边长 x 与面积S的函数关系是什么?其中自变量 x 的取值范围是什么?计算并填写下表:x0.511.522.533.5S面积 s 与边长 x 的函数关系式为: s = x2 (X>0)从式子 s = x2 来看,边长 x 越大,面积 s 也越大。能不能用图象直观的反映出来呢?大家思考一下,表示 x 与S的对应关系的点有多少个?如果全在坐标中指出的话是什么样子?可以讨论一下,然后发表你们的看法,建议大家不妨动手画画看. [生]这样的点有无数多个,如果全描出来太麻烦,也不可能.我们只能描出其中一部分,然后想象出其他点的位置,用光滑曲线连接起来. 函数图象可以数形结合地研究函数,给我们带来便利.由教师引导,学生观察得出结论,体现学生为主,教 师 为 主 导的关系.通 过 板书,突出本节课的重点.教 师 提1从函数图象可以看出,直线从左到右上升,即当 x 由小到大时,s = x2随之增大.根据表中数值描点(x,y),并用平滑曲线连接这些点(如上图). 观察上图: 一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.上图中的曲线即为函数S=x2(x>0)的图象.描点法画函数图象的一般步骤:第一步:列表.在自变量取值范围内选定一些值.通过函数关系式求出对应函数值列成表格.第二步:描点.在直角坐标系中,以自变量的值为横坐标,相应函数值为纵坐标,描出表中对应各点.第三步:连线.按照坐标由小到大的顺序把所有点用平滑曲线连结起来.教师提出问题,并引导学生归纳画函数图象的一般步骤.出问题,并...