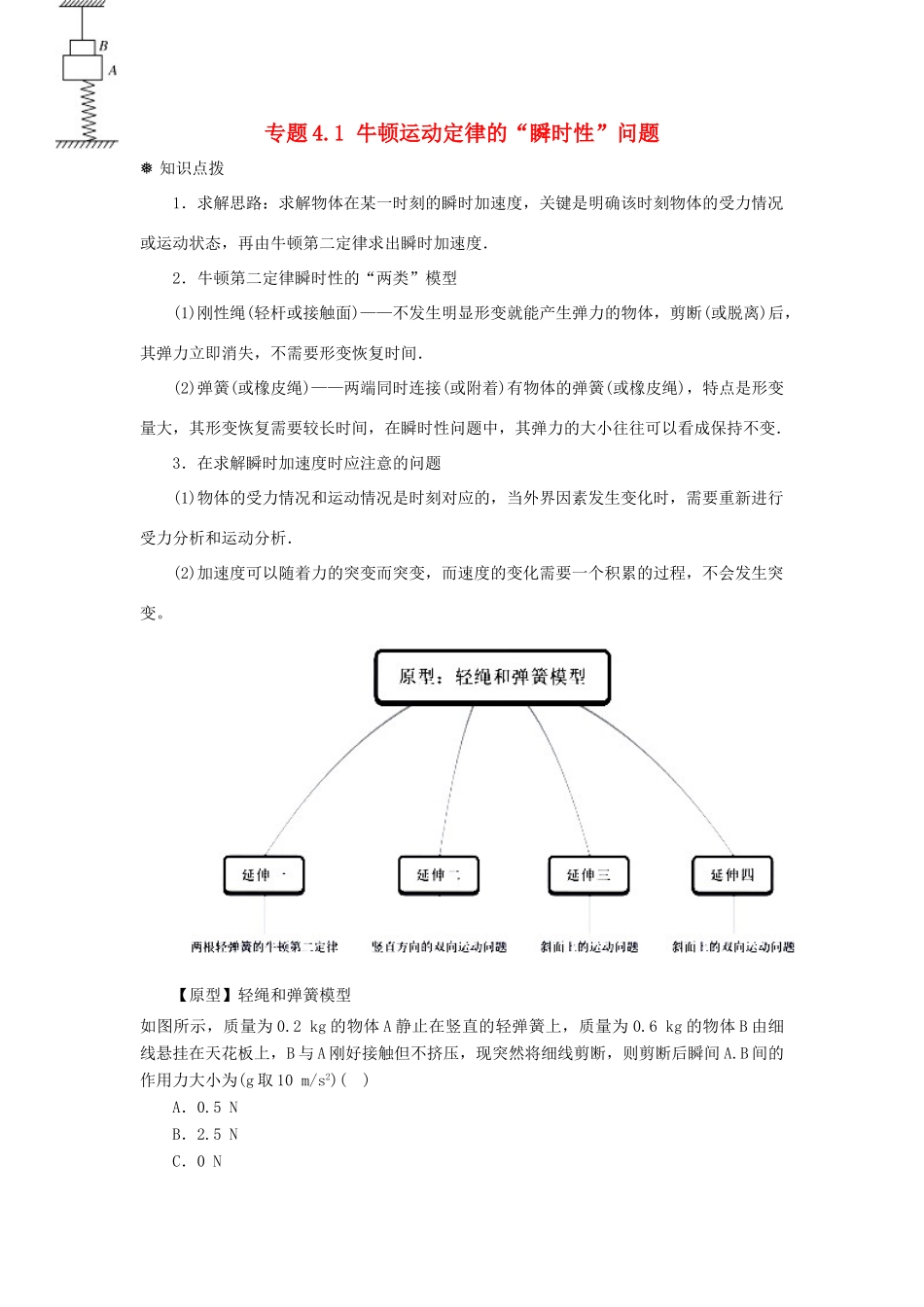
专题 4.1 牛顿运动定律的“瞬时性”问题❅ 知识点拨1.求解思路:求解物体在某一时刻的瞬时加速度,关键是明确该时刻物体的受力情况或运动状态,再由牛顿第二定律求出瞬时加速度.2.牛顿第二定律瞬时性的“两类”模型(1)刚性绳(轻杆或接触面)——不发生明显形变就能产生弹力的物体,剪断(或脱离)后,其弹力立即消失,不需要形变恢复时间.(2)弹簧(或橡皮绳)——两端同时连接(或附着)有物体的弹簧(或橡皮绳),特点是形变量大,其形变恢复需要较长时间,在瞬时性问题中,其弹力的大小往往可以看成保持不变.3.在求解瞬时加速度时应注意的问题(1)物体的受力情况和运动情况是时刻对应的,当外界因素发生变化时,需要重新进行受力分析和运动分析.(2)加速度可以随着力的突变而突变,而速度的变化需要一个积累的过程,不会发生突变。 【原型】轻绳和弹簧模型如图所示,质量为 0.2 kg 的物体 A 静止在竖直的轻弹簧上,质量为 0.6 kg 的物体 B 由细线悬挂在天花板上,B 与 A 刚好接触但不挤压,现突然将细线剪断,则剪断后瞬间 A.B 间的作用力大小为(g 取 10 m/s2)( )A.0.5 NB.2.5 NC.0 ND.1.5 N解析:剪断细线前,A、B 间无压力,则弹簧的弹力 F=mAg=0.2×10=2 N,剪断细线的瞬间,对整体★ 点评:本题是对弹簧和细线拉力特点与牛顿运动定律的综合考查,关键是对弹簧弹力的特点要有充分的认识,可以认为弹簧的弹力不会突变。 变型 1、两根轻弹簧的牛顿第二定律 【延伸 1】屋檐定时滴下水滴,当第 5 滴正欲滴下时,第 1 滴刚好到达地面,而第 3 滴与第2 滴正分别位于高为 1m 的窗户的上、下沿,如图所示,取 g=10m/s2。问:(1)滴水的时间间隔是多少? (2)此屋檐离地面多高? 解析:(1) ……………………………………(1)得 Δt=0.2s………………………………………………………………(2)(2)……………………………………………(3)★ 点评:解决本题的关键是掌握匀变速直线运动的位移-时间规律。 变型 2、竖直方向的双向运动问题 【延伸 2】从距地面高 h 处将一小球以初速度 v0=10m/s竖直向上抛出,经时间t=3s 落地,不计空气阻力,重力加速度 g=10m/s2,求: 小球落地时速度 v; 高度 h.解析:取竖直向上为正方向,则小球的加速度为 a=-g。小球落地时速度为:v=v0-gt=10-10× 30=-20 m/s2…………………(1)大小为 20 m/s2,方向竖直向下.小 球 的 位 ...