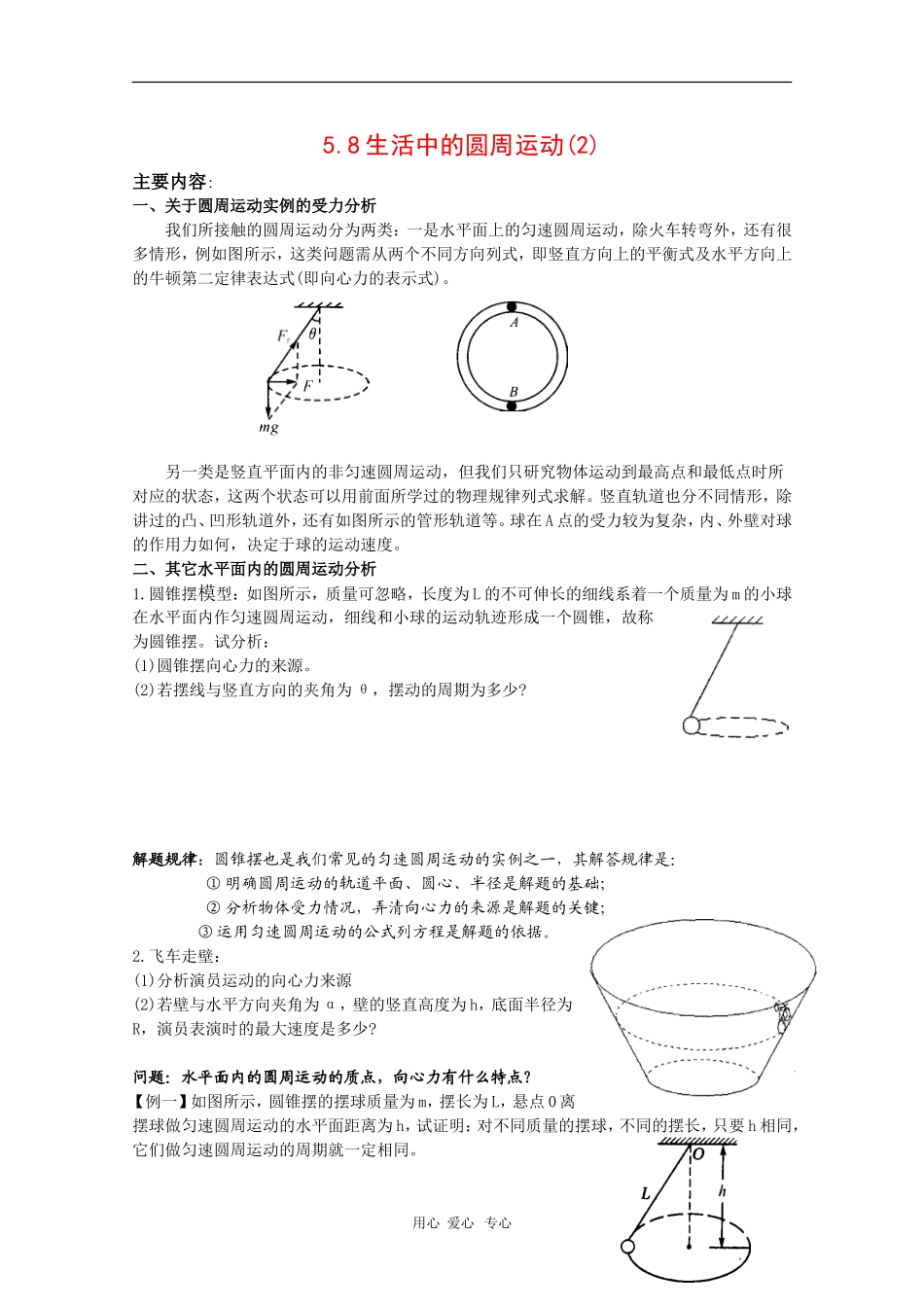
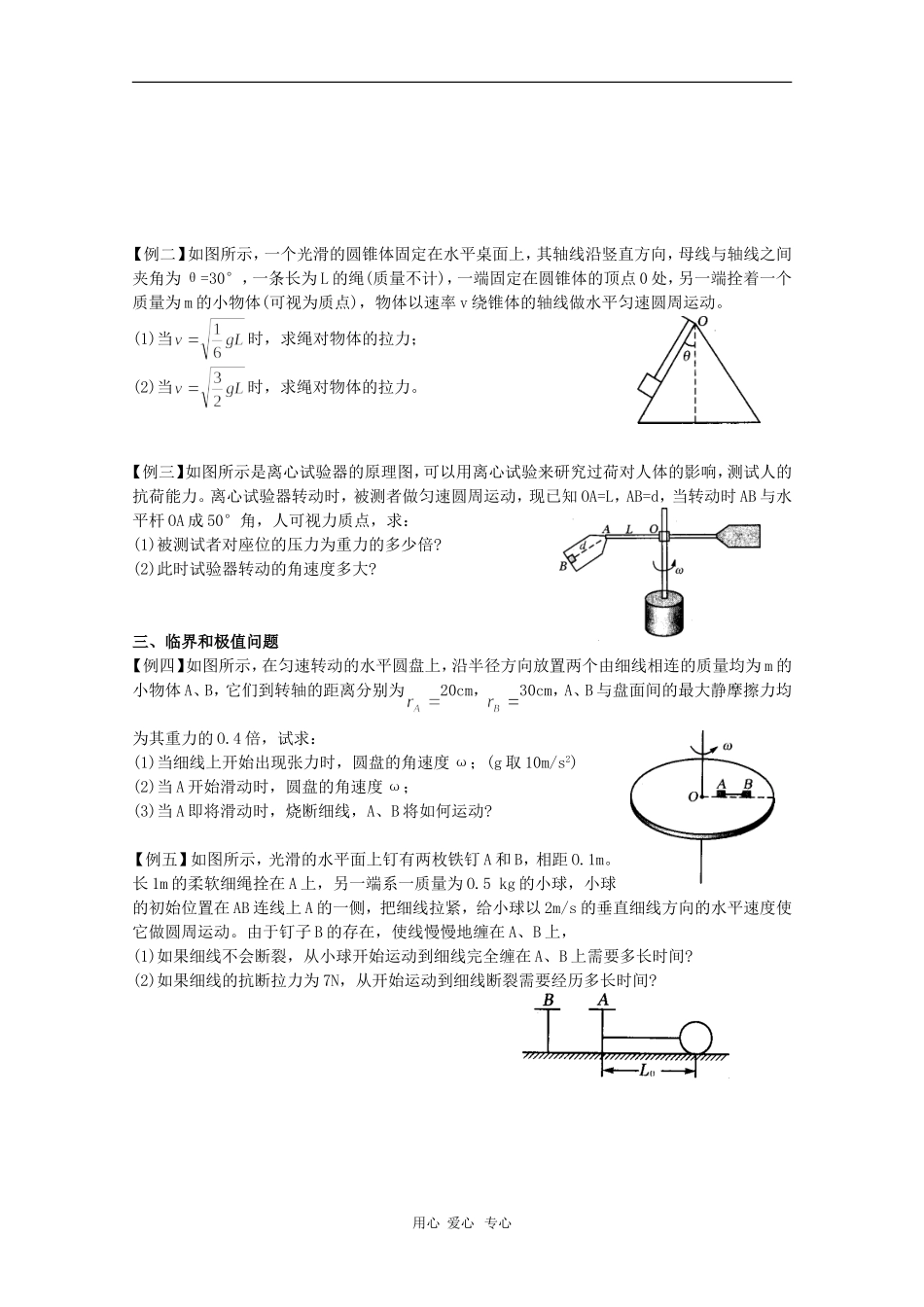
5.8 生活中的圆周运动(2)主要内容:一、关于圆周运动实例的受力分析我们所接触的圆周运动分为两类:一是水平面上的匀速圆周运动,除火车转弯外,还有很多情形,例如图所示,这类问题需从两个不同方向列式,即竖直方向上的平衡式及水平方向上的牛顿第二定律表达式(即向心力的表示式)。另一类是竖直平面内的非匀速圆周运动,但我们只研究物体运动到最高点和最低点时所对应的状态,这两个状态可以用前面所学过的物理规律列式求解。竖直轨道也分不同情形,除讲过的凸、凹形轨道外,还有如图所示的管形轨道等。球在 A 点的受力较为复杂,内、外壁对球的作用力如何,决定于球的运动速度。二、其它水平面内的圆周运动分析1.圆锥摆模型:如图所示,质量可忽略,长度为 L 的不可伸长的细线系着一个质量为 m 的小球在水平面内作匀速圆周运动,细线和小球的运动轨迹形成一个圆锥,故称为圆锥摆。试分析:(1)圆锥摆向心力的来源。(2)若摆线与竖直方向的夹角为 θ,摆动的周期为多少?解题规律:圆锥摆也是我们常见的匀速圆周运动的实例之一,其解答规律是: ① 明确圆周运动的轨道平面、圆心、半径是解题的基础; ② 分析物体受力情况,弄清向心力的来源是解题的关键;③ 运用匀速圆周运动的公式列方程是解题的依据。2.飞车走壁:(1)分析演员运动的向心力来源(2)若壁与水平方向夹角为 α,壁的竖直高度为 h,底面半径为R,演员表演时的最大速度是多少?问题:水平面内的圆周运动的质点,向心力有什么特点?【例一】如图所示,圆锥摆的摆球质量为 m,摆长为 L,悬点 0 离摆球做匀速圆周运动的水平面距离为 h,试证明:对不同质量的摆球,不同的摆长,只要 h 相同,它们做匀速圆周运动的周期就一定相同。用心 爱心 专心【例二】如图所示,一个光滑的圆锥体固定在水平桌面上,其轴线沿竖直方向,母线与轴线之间夹角为 θ=30°,一条长为 L 的绳(质量不计),一端固定在圆锥体的顶点 0 处,另一端拴着一个质量为 m 的小物体(可视为质点),物体以速率 v 绕锥体的轴线做水平匀速圆周运动。(1)当时,求绳对物体的拉力;(2)当时,求绳对物体的拉力。【例三】如图所示是离心试验器的原理图,可以用离心试验来研究过荷对人体的影响,测试人的抗荷能力。离心试验器转动时,被测者做匀速圆周运动,现已知 OA=L,AB=d,当转动时 AB 与水平杆 OA 成 50°角,人可视力质点,求:(1)被测试者对座位的压力为重力的多少倍?(2)此时试验器转动的...