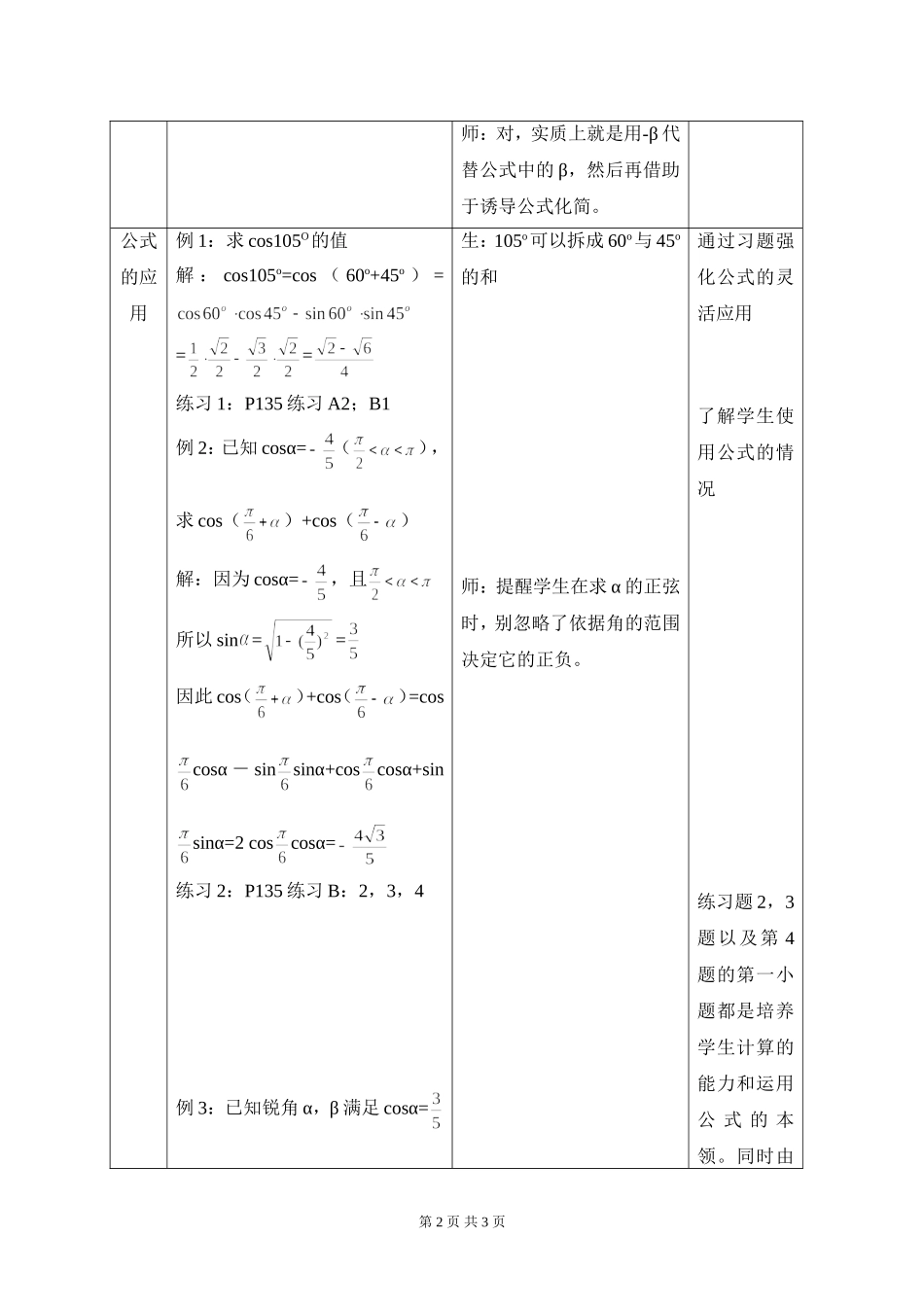
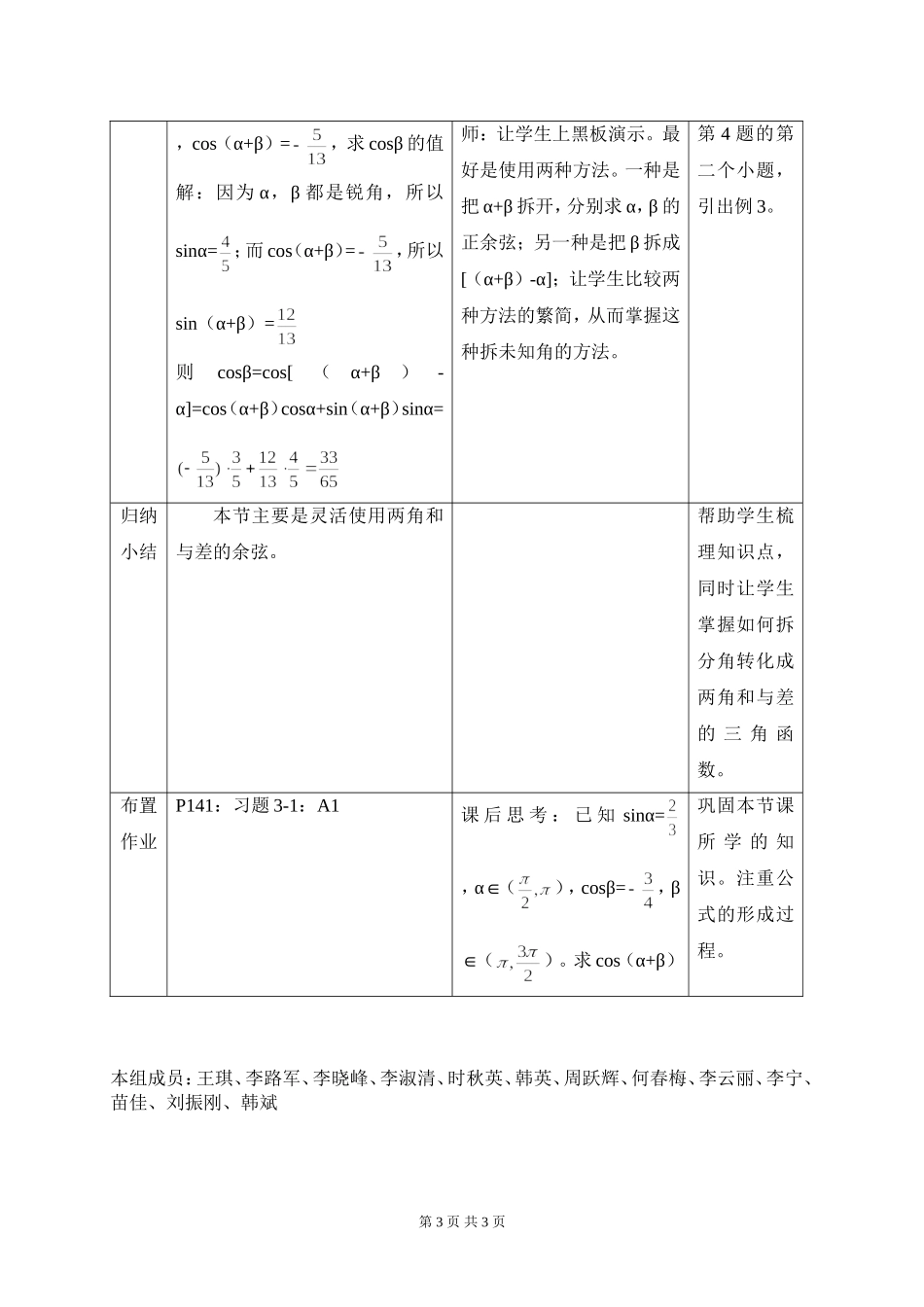
§3.1.1 两角和与差的余弦(二)(一)教学目标1、知识目标(1)利用两角差的余弦得到两角和的余弦(2)灵活正反运用两角和与差的余弦2、能力目标(1)通过两角差的余弦会转化成两角和的余弦,发现区别,转化区别,培养学生化未知为已知的能力。(2)培养学生灵活应用公式的能力。3、情感目标:通过对公式的灵活应用,培养学生融会贯通的能力。(二)教学重点、难点重点:两角和与差的余弦公式的灵活应用难点:(1)两角差的余弦过渡成两角和的余弦(2)两角和与差的灵活应用(三)教学方法练习讲解法(四)教学内容安排教学环节教学内容师生互动设计意图复习引入cos(α-β)=回忆两角差的余弦,学生回答,老师板书; 师:上节课我们留了一个思考题,“两角和的余弦公式”是什么?以旧带新,为引出新课程打基础。公式的推导以及理解公式 cos(α+β)的推导,以及公式的结构。cos(α+β)=cos[α-(-β)]==师:要解决的问题是两角和的余弦,而我们现在知道的是两角差的余弦,如何能把和 的 问 题 转 化 成 差 的 问题?生:把 α+β 写成 α-(-β)通过对问题的分析和提醒,使得学生有一个目标感。第 1 页 共 3 页师:对,实质上就是用-β 代替公式中的 β,然后再借助于诱导公式化简。公式的应用例 1:求 cos105O的值解 : cos105o=cos ( 60o+45o ) ===练习 1:P135 练习 A2;B1例 2:已知 cosα=(),求 cos()+cos()解:因为 cosα=,且所以 sin ==因此 cos()+cos()=coscosα - sinsinα+coscosα+sinsinα=2 coscosα=练习 2:P135 练习 B:2,3,4例 3:已知锐角 α,β 满足 cosα=生:105o可以拆成 60o与 45o的和师:提醒学生在求 α 的正弦时,别忽略了依据角的范围决定它的正负。通过习题强化公式的灵活应用了解学生使用公式的情况练习题 2,3题以及第 4题的第一小题都是培养学生计算的能力和运用公 式 的 本领。同时由第 2 页 共 3 页,cos(α+β)=,求 cosβ 的值解:因为 α,β 都是锐角,所以sinα=;而 cos(α+β)=,所以sin(α+β)=则cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=师:让学生上黑板演示。最好是使用两种方法。一种是把 α+β 拆开,分别求 α,β 的正余弦;另一种是把 β 拆成[(α+β)-α];让学生比较两种方法的繁简,从而掌握这种拆未知角的方法。第 4 题的第二个小题,引出例 3。归纳...