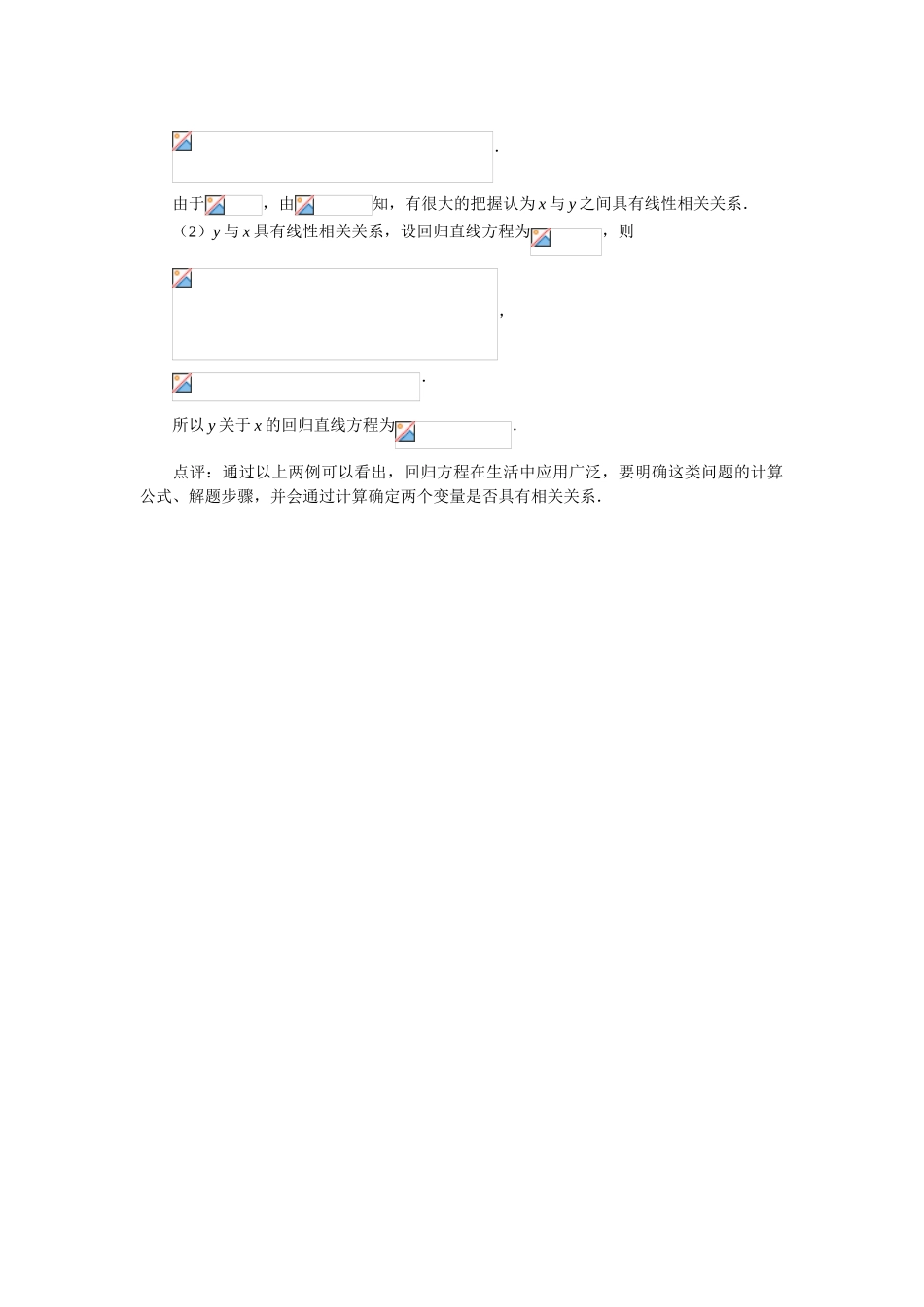
线性回归中的相关系数 线性回归问题在生活中应用广泛,求解回归直线方程时,应该先推断两个变量是否是线性相关,若相关再求其直线方程,推断两个变量有无相关关系的一种常用的简便方法是绘制散点图;另外一种方法是量化的检验法,即相关系数法.下面为同学们介绍相关系数法. 一、关于相关系数法 统计中常用相关系数 r 来衡量两个变量之间的线性相关的强弱,当不全为零,yi也不全为零时,则两个变量的相关系数的计算公式是: r 就叫做变量 y 与 x 的相关系数(简称相关系数). 说明:(1)对于相关系数 r,首先值得注意的是它的符号,当 r 为正数时,表示变量x,y 正相关;当 r 为负数时,表示两个变量 x,y 负相关; (2)另外注意 r 的大小,假如,那么正相关很强;假如,那么 负 相 关 很 强 ; 假 如或, 那 么 相 关 性 一 般 ; 假 如,那么相关性较弱. 下面我们就用相关系数法来分析身边的问题,确定两个变量是否相关,并且求出两个变量间的回归直线. 二、典型例题剖析 例 1 测得某国 10 对父子身高(单位:英寸)如下:父亲身高()60626465666768707274儿子身高()63.565.26665.566.967.167.468.370.170 (1)对变量 y 与 x 进行相关性检验; (2)假如 y 与 x 之间具有线性相关关系,求回归直线方程; (3)假如父亲的身高为 73 英寸,估量儿子身高. 解 : ( 1 ),,,,,,,, 所以, 所以 y 与 x 之间具有线性相关关系. (2)设回归直线方程为,则,. 故所求的回归直线方程为. (3)当英寸时,, 所以当父亲身高为 73 英寸时,估量儿子的身高约为 69.9 英寸. 点评:回归直线是对两个变量线性相关关系的定量描述,利用回归直线,可以对一些实际问题进行分析、预测,由一个变量的变化可以推测出另一个变量的变化.这是此类问题常见题型. 例 2 10 名同学在高一和高二的数学成绩如下表:7471726876736770657476757170767965776272 其中 x 为高一数学成绩,y 为高二数学成绩. (1)y 与 x 是否具有相关关系; (2)假如 y 与 x 是相关关系,求回归直线方程. 解:(1)由已知表格中的数据,利用计算器进行计算得 ,,,,.,.. 由于,由知,有很大的把握认为 x 与 y 之间具有线性相关关系. (2)y 与 x 具有线性相关关系,设回归直线方程为,则 ,. 所以 y 关于 x 的回归直线方程为. 点评:通过以上两例可以看出,回归方程在生活中应用广泛,要明确这类问题的计算公式、解题步骤,并会通过计算确定两个变量是否具有相关关系.