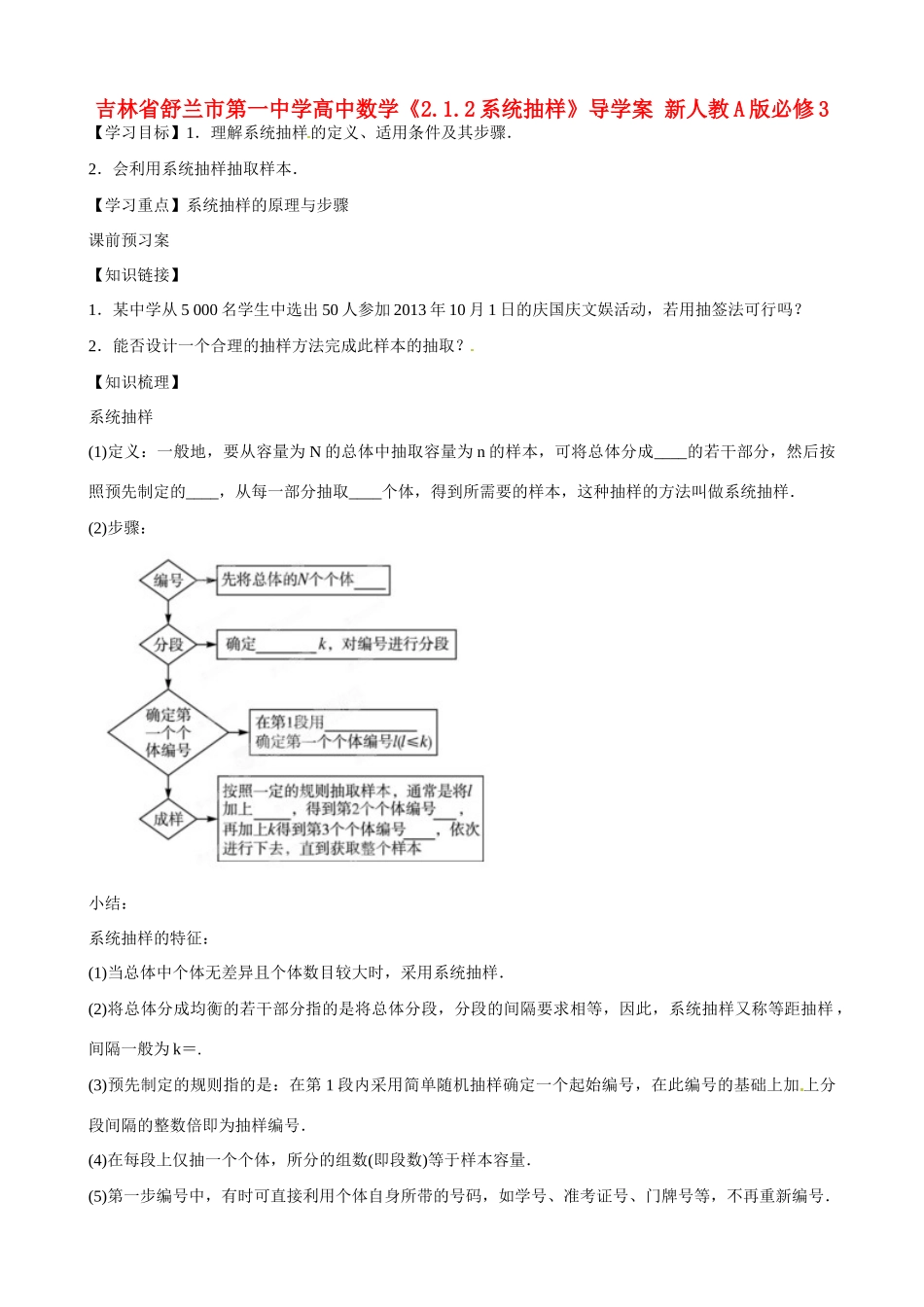
吉林省舒兰市第一中学高中数学《2.1.2 系统抽样》导学案 新人教 A 版必修 3【学习目标】1.理解系统抽样的定义、适用条件及其步骤.2.会利用系统抽样抽取样本.【学习重点】系统抽样的原理与步骤课前预习案【知识链接】1.某中学从 5 000 名学生中选出 50 人参加 2013 年 10 月 1 日的庆国庆文娱活动,若用抽签法可行吗?2.能否设计一个合理的抽样方法完成此样本的抽取?【知识梳理】系统抽样(1)定义:一般地,要从容量为 N 的总体中抽取容量为 n 的样本,可将总体分成____的若干部分,然后按照预先制定的____,从每一部分抽取____个体,得到所需要的样本,这种抽样的方法叫做系统抽样.(2)步骤:小结:系统抽样的特征:(1)当总体中个体无差异且个体数目较大时,采用系统抽样.(2)将总体分成均衡的若干部分指的是将总体分段,分段的间隔要求相等,因此,系统抽样又称等距抽样 ,间隔一般为 k=.(3)预先制定的规则指的是:在第 1 段内采用简单随机抽样确定一个起始编号,在此编号的基础上加 上分段间隔的整数倍即为抽样编号.(4)在每段上仅抽一个个体,所分的组数(即段数)等于样本容量.(5)第一步编号中,有时可直接利用个体自身所带的号码,如学号、准考证号、门牌号等,不再重新编号.2.系统抽样中的合理分段问题说明:系统抽样操作的要领是先将个体数较多的总体分成均衡的若干部分,然后按照预先制定的规则,从每一部分中抽取 1 个个体,从而得到所需的样本.由于抽样的间隔相等,因此系统抽样又称为等距抽样(或叫机械抽样),所以系统抽样中必须对总体中的每个个体进行合理(即等距)分段.(1)若从容量为 N 的总体中抽取容量为 n 的样本,用系统抽样时,应先将总体中的各个个体编号,再确定分段间隔 k,以便对总体进行分段.(2)当是整数时,取 k=作为分段间隔即可,如 N=100,n=20,则分段间隔 k==5.也就是将 100 个个体按平均每 5 个为 1 段(组)进行分段(组);(3)当不是整数时,应先从总体中随机剔除一些个体,使剩余个体数 N′能被 n 整除,这时分段间隔 k=,如 N=101,n=20,则应先用简单随机抽样从总体中剔除 1 个个体,使剩余的总体容量(即 100)能被20 整除,从而得出分段间隔 k==5,也就是说,只需将 100 个个体平均分为 20 段(组).(4)一般地,用简单随机抽样的方法从总体中剔除部分个体,其个数为总体中的个体数除以样本容量所得的余数.自主小测:1、 中央电视台动...