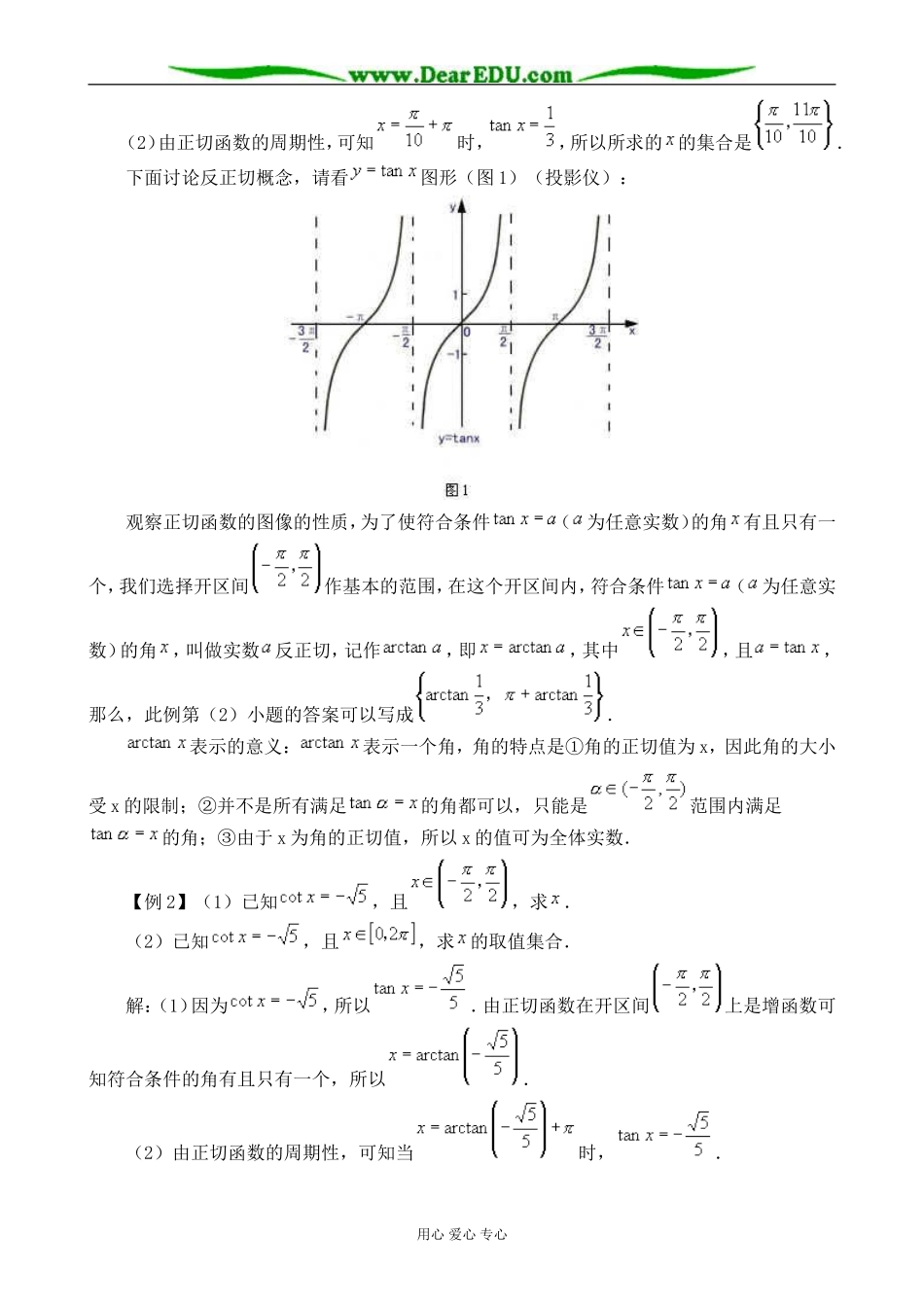
已知三角函数值求角一、教学目标 1.掌握已知一角的正切值,求角的方法. 2.掌握给定区间内,用反三角函数表示一个角的方法.二、教学具准备 投影仪三、教学过程 1.设置情境 师:请同学们看投影,回答问题 (1)若,,则. (2)若,则. 生:(1)或. (2)或. 师:回答正确.请同学结合上面两个小题的求解过程,总结一下已知三角函数值求角的一般步骤: 生:从上面两个小题的求解过程看,有三个步骤: 第一步,决定角可能是第几象限角. 第二步,如果函数值为正数,则先求出对应的锐角;如果函数值为负数,则先求了与其绝对值对应的锐角; 第三步,如果函数值为负数,则根据角可能是第几象限角,得出内对应的角—如果它是第二象限角,那么可表示为,如果它是第三或第四象限角,那么可表示为或. 师:总结得很好,本节课我们继续学习用反正切表示角的方法,先请同学看问题(投影仪) 2.探索研究(此部分可由学生仿照正弦、余弦分析解决) 【例 1】(1)已知,且,求(精确到). (2)已知,且,求的取值集合. 解:(1)由正切函数在开区间上是增函数和可知,符合条件的角有且只有一个,利用计算器可得(或).用心 爱心 专心 (2)由正切函数的周期性,可知时,,所以所求的的集合是. 下面讨论反正切概念,请看图形(图 1)(投影仪): 观察正切函数的图像的性质,为了使符合条件(为任意实数)的角有且只有一个,我们选择开区间作基本的范围,在这个开区间内,符合条件(为任意实数)的角,叫做实数反正切,记作,即,其中,且,那么,此例第(2)小题的答案可以写成. 表示的意义:表示一个角,角的特点是①角的正切值为 x,因此角的大小受 x 的限制;②并不是所有满足的角都可以,只能是范围内满足的角;③由于 x 为角的正切值,所以 x 的值可为全体实数. 【例 2】(1)已知,且,求. (2)已知,且,求的取值集合. 解:(1)因为,所以.由正切函数在开区间上是增函数可知符合条件的角有且只有一个,所以. (2)由正切函数的周期性,可知当时,.用心 爱心 专心 ∴所求的取值集合是.参考例题(供层次高的学生使用): 1.求值. 解:根据诱导公式,且, ∴. 评法:由于反正弦表示内的一个角,而,所以应先用诱导公式将其转化为区间内的角,再进行计算. 2.求的值. 解: 、表示中的角 ∴令,则, ,则 ∴ 又 和均为锐角 ∴ ∴ 3.演练反馈(投影) (1)满足的的...