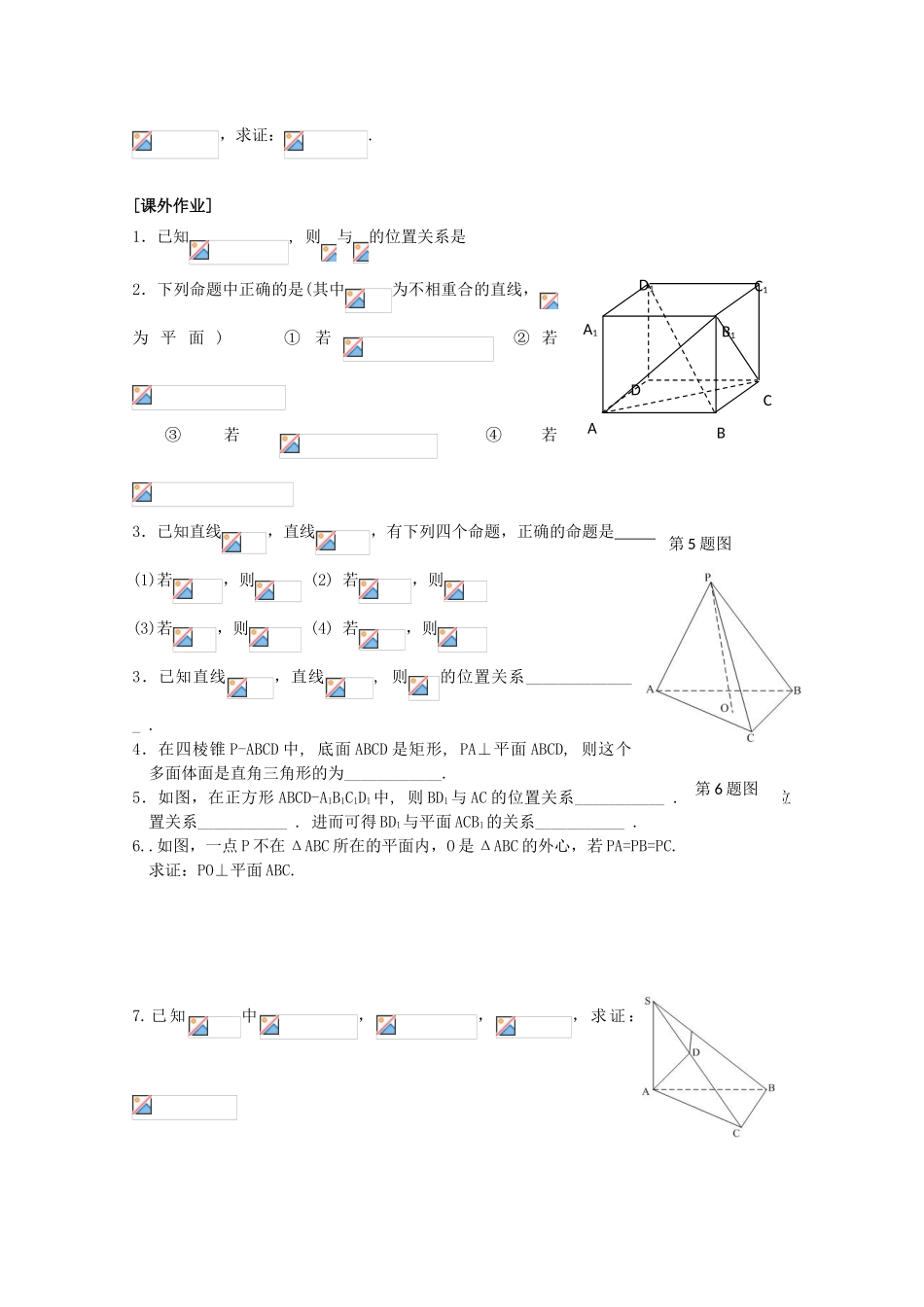
[课题] 直线与平面的位置关系(2)[学习要求]1.掌握直线与平面的位置关系.2.掌握直线和平面垂直的判定与性质定理.3.应用直线和平面垂直的判定和性质定理证明两条直线垂直等有关问题. [知识体系]1.直线和平面垂直的定义: 符号表示: 垂线: 垂面: 垂足: 思考:在平面中,过一点有且仅有一条直线与已知直线垂直,那么在空间.(1)过一点有几条直线与已知平面垂直? (2)过一点有几条平面与已知直线垂直?2.定理:过一点有且只有一条直线与已知平面垂直,过一点有且只有一个平面与已知直线垂直3.点到平面的距离: 4.直线与平面垂直的判定定理: 符号表示 5.直线和平面垂直的性质定理: 6.直线和平面的距离: [例题解析]例 1:求证: 如果两条平行直线中的一条垂直于一个平面, 那么另一条直线也垂直于这个平面.例 2:如图, 已知, 垂足分别为且, 求证:例 3 : 已 知 正 方 体, (1) 求 证 :;(2) 若分 别 为与上 的 点 , 且,ABCDD1A1C1B1,求证:.[课外作业]1.已知, 则与的位置关系是 2.下列命题中正确的是(其中为不相重合的直线,为 平 面 ) ①若 ② 若③若 ④若3.已知直线,直线,有下列四个命题,正确的命题是 (1)若,则 (2) 若,则 (3)若,则 (4) 若,则3.已知直线,直线, 则的位置关系______________ .4.在四棱锥 P-ABCD 中, 底面 ABCD 是矩形, PA⊥平面 ABCD, 则这个多面体面是直角三角形的为____________.5.如图,在正方形 ABCD-A1B1C1D1中, 则 BD1与 AC 的位置关系___________ . BD1与 B1C 的位置关系___________ . 进而可得 BD1与平面 ACB1的关系___________ .6..如图,一点 P 不在 ΔABC 所在的平面内,O 是 ΔABC 的外心,若 PA=PB=PC.求证:PO⊥平面 ABC.7.已知中,,,求证 :第 5 题图第 6 题图