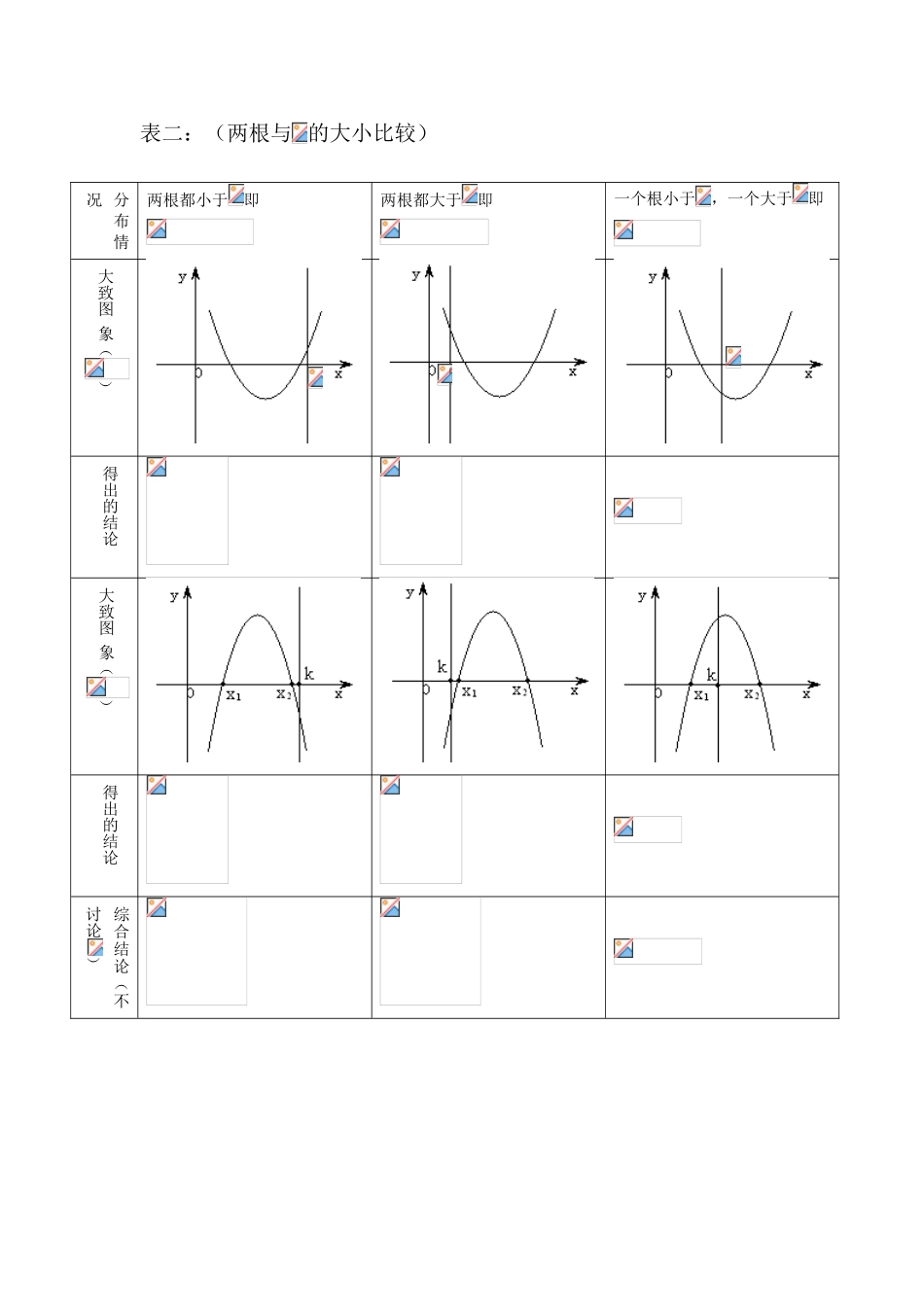
二次函数根的分布一、知识点二次方程根的分布与二次函数在闭区间上的最值归纳一元二次方程根的分布情况表一:(两根与 0 的大小比较即根的正负情况)分布情况两个负根即两根都小于 0两个正根即两根都大于 0一正根一负根即一个根小于0,一个大于 0大致图 象()得出的结论大致图 象()得出的结论综合结论(不讨论)表二:(两根与 的大小比较)分布情况两根都小于即两根都大于即一个根小于,一个大于即大致图 象()得出的结论大致图 象()得出的结论综合结论(不讨论)表三:(根在区间上的分布)二、经典例题例 1:(实根与分布条件)已知是方程的两个根,且分布情况两根都在内两根有且仅有一根在内(图象有两种情况,只画了一种)一 根 在内 , 另 一 根 在内,大致图 象()得出的结论或大致图 象()得出的结论或综合结论(不讨论——————,求实数的取值范围。变式:关于的方程的两个根,一个小于 0,一个大于 1,求的取值范围。例 2:(动轴定区间)函数在区间上是单调函数,则的取值范围是变式 2:函数在上是增函数,求实数的取值范围。列 3:(定轴动区间)求函数在上的值域。变式 3:已知函数在区间上有最小值 3,求实数的取值范围。例 4:(定轴动区间)已知二次函数,若在上的最小值为,求的表达式。变式 4:已知二次函数满足,且,若在区间上的值域是,求的值。例 5:(恒成立问题)已知函数,若对于任意,都有成立,求实数的取值范围。变式 5:已知函数在上恒大于 0,求实数的取值范围。三、课后练习1、已知二次方程有一正根和一负根,求实数的取值范围。2、函数在上有最大值 5 和最小值 2,求的值。3、讨论函数的最小值。4、已知函数的图像与x 轴的交点至少有一个在原点的右侧,求实数 m的取值范围。5、已知函数,当时,恒成立,求的取值范围。