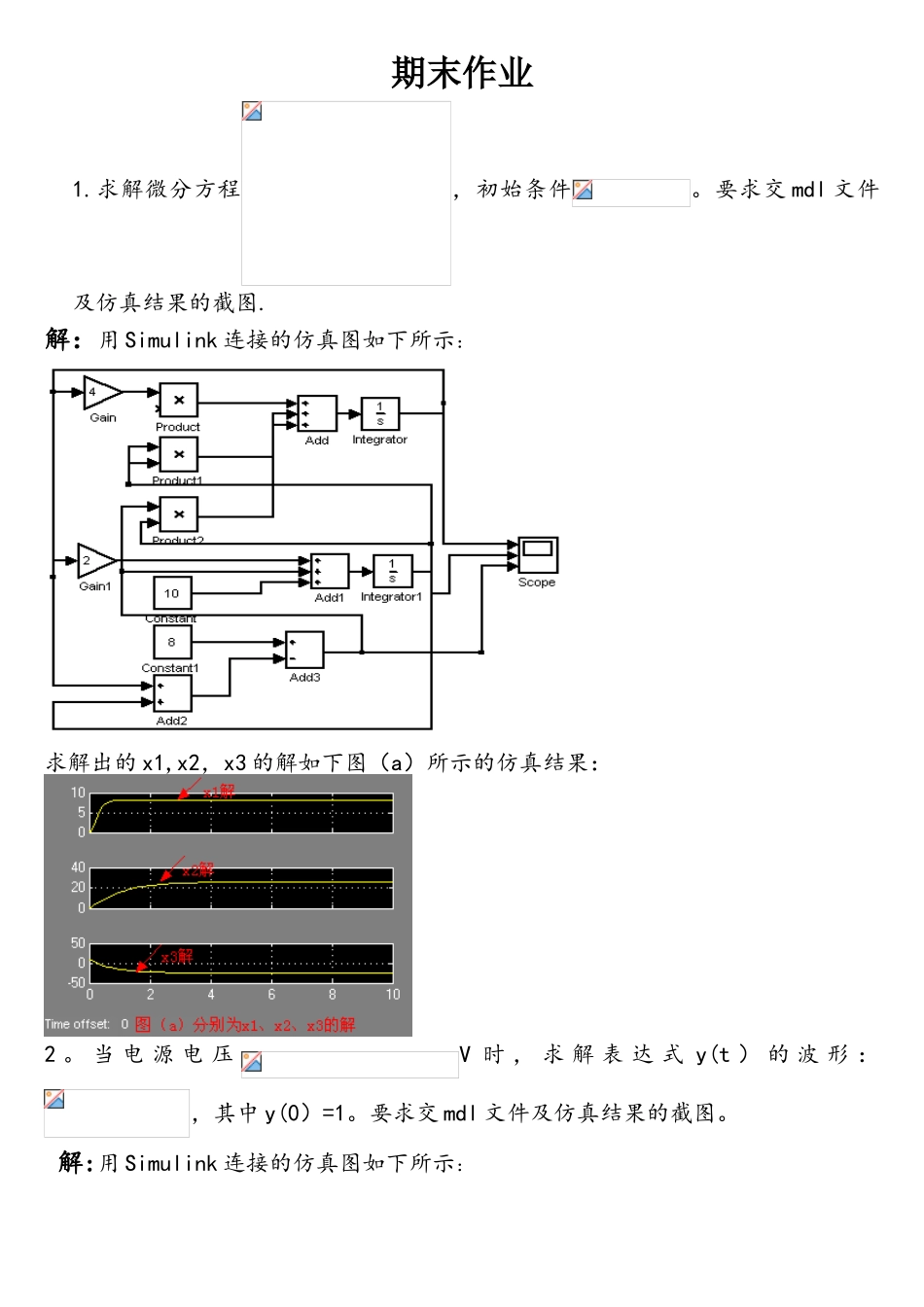
期末作业1.求解微分方程,初始条件。要求交 mdl 文件及仿真结果的截图.解:用 Simulink 连接的仿真图如下所示:求解出的 x1,x2,x3 的解如下图(a)所示的仿真结果:2 。 当 电 源 电 压V 时 , 求 解 表 达 式 y(t ) 的 波 形 :,其中 y(0)=1。要求交 mdl 文件及仿真结果的截图。解:用 Simulink 连接的仿真图如下所示:仿真结果如下图(b)所示:3。使用 S 函数实现 y=5*x+3,建立仿真模型并得出仿真结果.要求交 mdl 文件,S函数及仿真结果的截图。解:用 Simulink 连接的仿真图如下所示:S 函数的代码如下:function [sys,x0,str,ts] = mysfun3 (t,x,u,flag)switch flag,case 0, [sys,x0,str,ts]=mdlInitializeSizes; case 1, sys=mdlDerivatives(t,x,u); case 2, sys=mdlUpdate(t,x,u);case 3, sys=mdlOutputs(t,x,u);case 4, sys=mdlGetTimeOfNextVarHit(t,x,u);case 9, sys=mdlTerminate(t,x,u);otherwise error([’Unhandled flag = ',num2str(flag)]);endfunction [sys,x0,str,ts]=mdlInitializeSizessizes = simsizes;sizes。NumContStates = 0;sizes.NumDiscStates = 0;sizes.NumOutputs = 1;sizes。NumInputs = 1;sizes。DirFeedthrough = 1;sizes。NumSampleTimes = 1; sys = simsizes(sizes);x0 = [];str = [];ts = [0 0];function sys=mdlDerivatives(t,x,u)sys = [];function sys=mdlUpdate(t,x,u)sys = [];function sys=mdlOutputs(t,x,u)sys = 5*u+3;function sys=mdlGetTimeOfNextVarHit(t,x,u)sampleTime = 1; sys = t + sampleTime;function sys=mdlTerminate(t,x,u)sys = [];仿真结果如下图(c)所示:4.已知某系统的状态方程如下:试用 S 函数建立其仿真模型,并求其单位阶跃响应曲线.解:用 Simulink 连接的仿真图如下所示: S 函数的代码如下:function [sys,x0,str,ts] =mysfun4(t,x,u,flag)switch flag, case 0, [sys,x0,str,ts]=mdlInitializeSizes; case 1, sys=mdlDerivatives(t,x,u); case 2, sys=mdlUpdate(t,x,u); case 3, sys=mdlOutputs(t,x,u); case 4, sys=mdlGetTimeOfNextVarHit(t,x,u); case 9, sys=mdlTerminate(t,x,u); otherwise DAStudio。error('Simulink:blocks:unhandledFlag', num2str(flag)); endfunction [sys,x0,str,ts]=mdlInitializeSizessizes = simsizes;sizes。NumContStates = 3;sizes.NumDiscStates = 0;sizes.NumOutputs = 1;sizes。NumInputs = 1;sizes.DirFeedthrough = 0;sizes.NumSampleTimes = 1; sys = simsizes(sizes);x0 = [0;0;0]; str = [];ts = [0 0];function sys=mdlDerivatives(t,x,u)x(1)=1*x(1)-1*x(2)-2*x(3)+u;x(2)=2*x(2)-1*x(3);x(3)=3*x(3)+u;sys =x;function sys=mdlUpdate(t,x,u)sys = [];function sys=mdlOutputs(t,x,u)sys = 1*x(1)-2*x(2)+3*x(3);function sys=mdlGetTimeOfNextVarHit(t,x,u)sampleTime = 1; sys = t + sampleTime;function sys=mdlTerminate(t,x,u)sys = [];仿真结果如下图(d)所示: