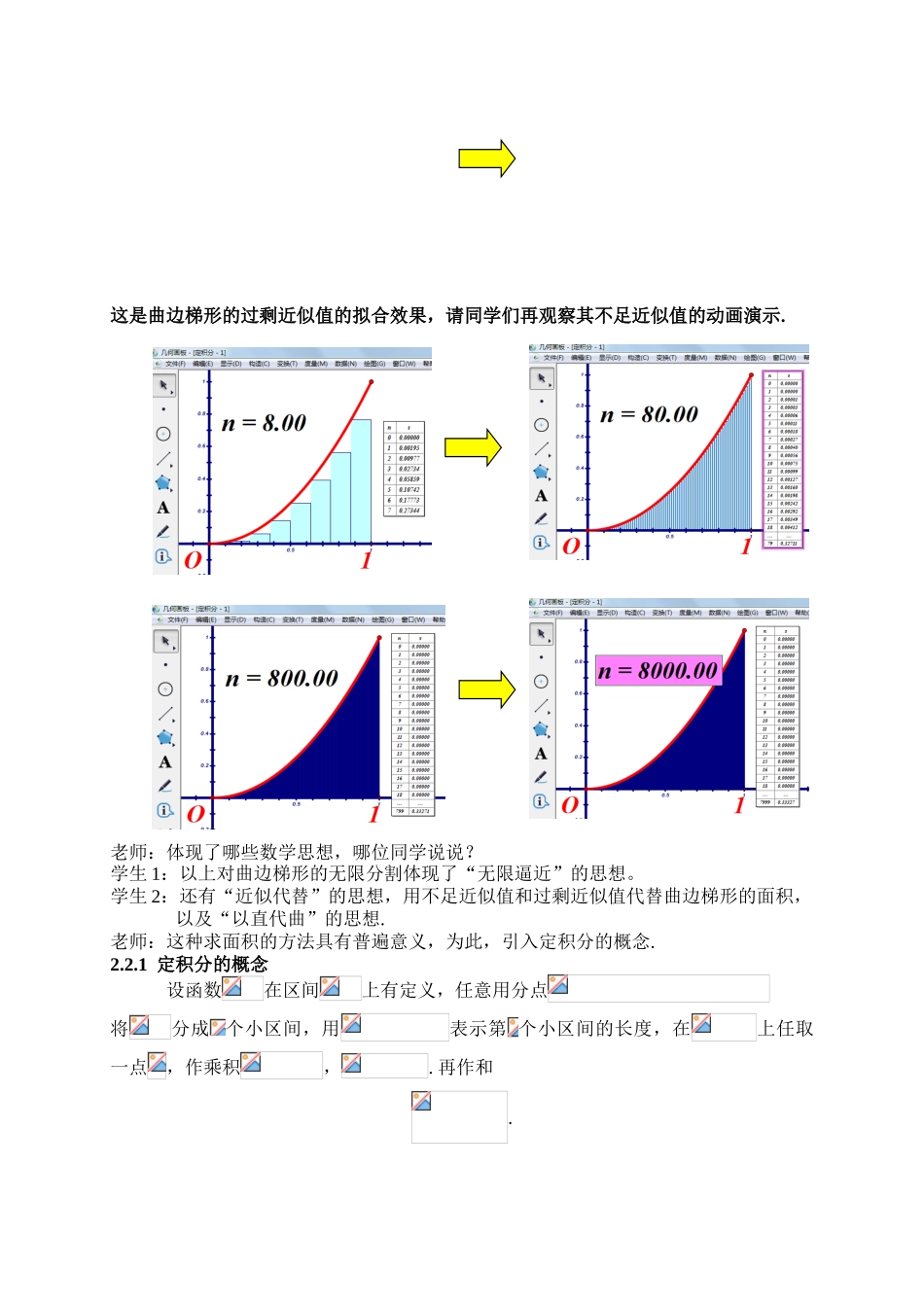
《定积分的概念》教学案例设计1 教学目标及重点、难点1.1 教学目标知识目标:1.通过求曲边梯形的面积和变速直线运动的路程,了解定积分概念的实际背景意义;2.借助于几何直观理解定积分的基本思想,了解定积分的概念,会应用定积分的定义求函数的定积分.3.理解掌握定积分的几何意义和性质;能力目标:体会“以直代曲”,“无限逼近”,“近似代替”等数学思想.情感态度价值观:体会定积分在实际问题中的应用,体会数学的强大威力.1.2教学重点微元法思想和定积分的基本性质1.3教学难点无限细分和无穷累积的思维方法2 教学过程简录2.1 实例铺路,引出课题 老师:“回忆前面曲边图形面积,变速运动的路程,变力做功等问题的解决方法,解决步骤是什么?” 学生:分割→以直代曲→求和→取极限(逼近) 老师:“对这四个步骤再以分析、理解、归纳,找出共同点.”师生共同归纳得出,以上两个例子尽管来自不同领域,却都归结为求同一结构的和式的极限. 我们以后还将看到,在求变力所作的功、水压力、某些空间体的体积等许多问题中,都会出现这种形式的极限,因此,有必要在数学上统一对它们进行讨论.2.2演示验证,直观感知老师:“让我们再次回顾解决曲边梯形的面积的方法,体会当中蕴含的数学思想.”(老师动画演示对曲边梯形的分割过程)这是曲边梯形的过剩近似值的拟合效果,请同学们再观察其不足近似值的动画演示.老师:体现了哪些数学思想,哪位同学说说?学生 1:以上对曲边梯形的无限分割体现了“无限逼近”的思想。学生 2:还有“近似代替”的思想,用不足近似值和过剩近似值代替曲边梯形的面积,以及“以直代曲”的思想.老师:这种求面积的方法具有普遍意义,为此,引入定积分的概念.2.2.1 定积分的概念 设函数在区间上有定义,任意用分点将分成个小区间,用表示第 个小区间的长度,在上任取一点,作乘积,. 再作和.图 5 - 1a=x0 x1 x2 xi-1 xi xn-1 xn =biOn1 2y=f(x)xy若当时,上式的极限存在,则称函数在区间上可积,并称此极限值为在上的定积分,记作. 即 . (1)其中称为被积函数,称为被积表达式,称为积分变量,称为积分区间,分别称为积分下限和上限.许多实际问题都可用定积分表示. 例如,若变速直线运动的速度为,则在时间区间上,物体经过的路程为 . (2)同理,图 5-1 所示的曲边梯形面积可表为 (3)变力做功 (4)I.在可积,是指不管对区间分划的方式怎样,也不管点在小区间上如何选取,...