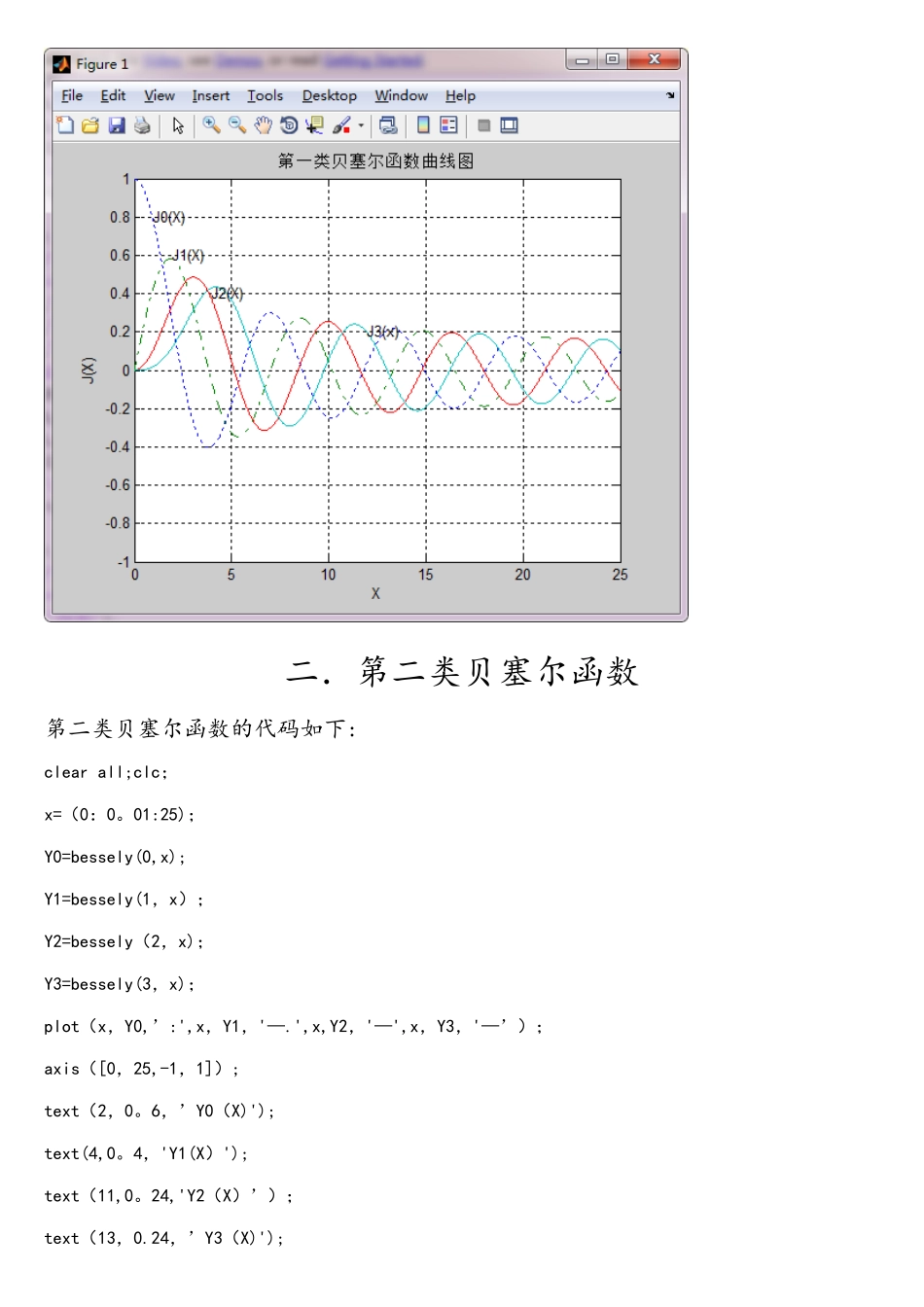
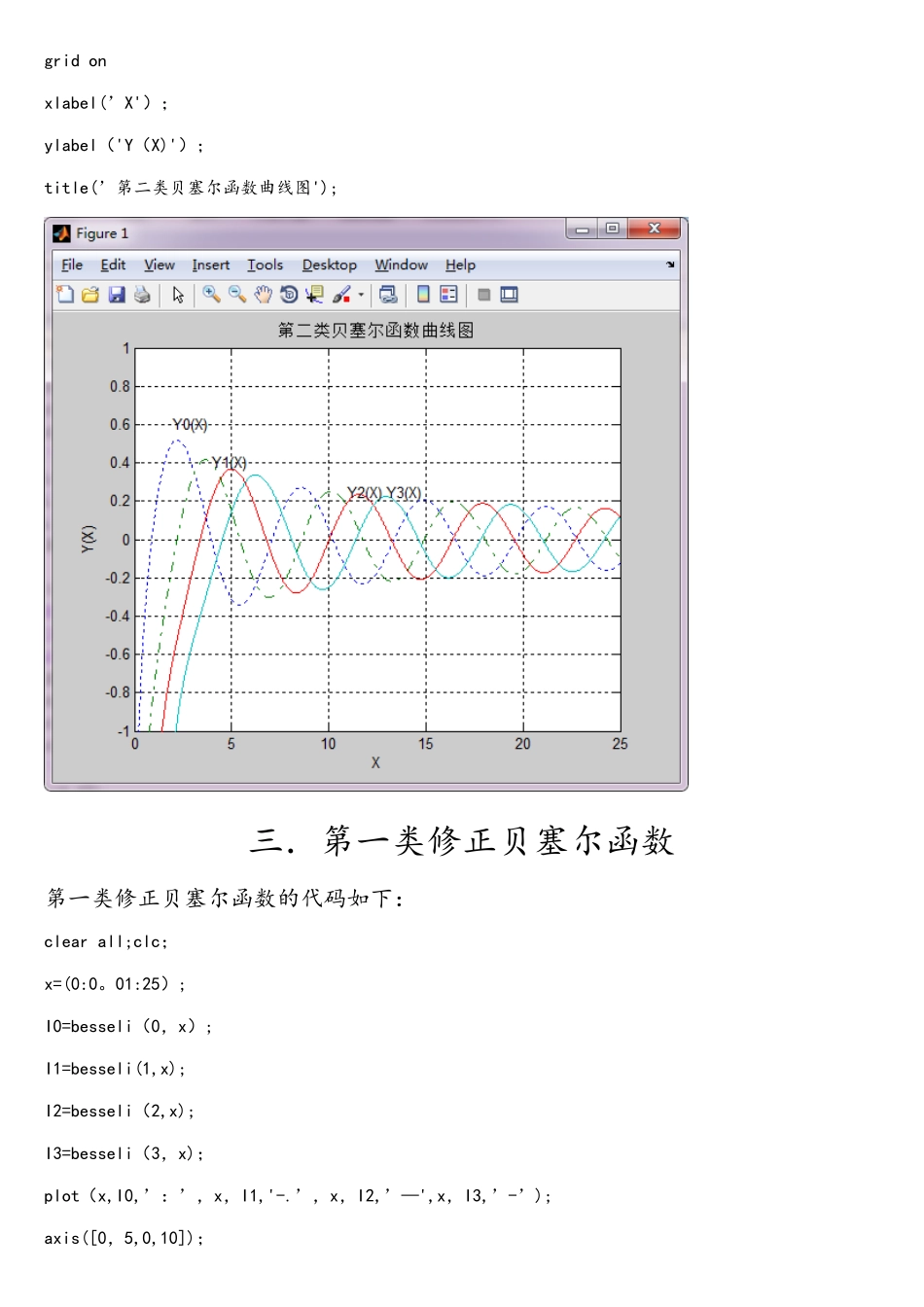
一.第一类贝塞尔函数第一类贝塞尔函数的代码如下:clear allx=(0:0.01:25);J0=besselj(0,x);J1=besselj(1,x);J2=besselj(2,x);J3=besselj(3,x);plot(x,J0,’:’,x,J1,’-.',x,J2,’—’,x,J3,’—');axis([0,25,—1,1]);grid onxlabel('X');ylabel(’J(X)');title(’第一类贝塞尔函数曲线图');text(1,0。8,'J0(X)’);text(2,0.6,'J1(X)’);text(4,0.4,’J2(X)’);text(12,0。2,’J3(x)');二.第二类贝塞尔函数第二类贝塞尔函数的代码如下:clear all;clc;x=(0:0。01:25);Y0=bessely(0,x);Y1=bessely(1,x);Y2=bessely(2,x);Y3=bessely(3,x);plot(x,Y0,’:',x,Y1,'—.',x,Y2,'—',x,Y3,'—’);axis([0,25,-1,1]);text(2,0。6,’Y0(X)');text(4,0。4,'Y1(X)');text(11,0。24,'Y2(X)’);text(13,0.24,’Y3(X)');grid onxlabel(’X');ylabel('Y(X)');title(’第二类贝塞尔函数曲线图');三.第一类修正贝塞尔函数第一类修正贝塞尔函数的代码如下:clear all;clc;x=(0:0。01:25);I0=besseli(0,x);I1=besseli(1,x);I2=besseli(2,x);I3=besseli(3,x);plot(x,I0,’:’,x,I1,'-.’,x,I2,’—',x,I3,’-’);axis([0,5,0,10]);text(0.5,1.3,'I0(X)');text(2。5,2,’I1(X)');text(3.5,3.1,'I2(X)');text(4.4,5,'I3(X)');grid onxlabel(’X’);ylabel('I(X)’);title(’第一类修正贝塞尔函数曲线图');四.第二类修正贝塞尔函数第二类修正贝塞尔函数的代码如下:clear all;clc;x=(0:0。01:20);K0=besselk(0,x);K1=besselk(1,x);K2=besselk(2,x);K3=besselk(3,x);plot(x,K0,':’,x,K1,’—.',x,K2,’—’,x,K3,'-');axis([0,5,0,10]);text(0.5,0。5,'K0(X)');text(0。3,3。5,'K1(X)');text(1,2,'K2(X)’);text(1。8,1,'K3(X)’);grid onxlabel('X’);ylabel('K(X)');title(’第二类修正贝塞尔函数曲线图’);五.阶跃函数阶跃函数的代码如下:clear allclc;format longha=[0:0.01:12];a=[0:0.001:2];b=[0:0。001:5];c=[0:0.001:8];y=ha.*besselj(1,ha)。/besselj(0,ha);y1=sqrt(4—a。^2).*besselk(1,sqrt(4—a.^2))./besselk(0,sqrt(4—a。^2));y2=sqrt(25-b.^2)。*besselk(1,sqrt(25-b。^2))./besselk(0,sqrt(25—b。^2));y3=sqrt(64—c.^2)。*besselk(1,sqrt(64-c.^2))./besselk(0,sqrt(64-c.^2));h=plot(ha,y,’k-',a,y1,'r-’,b,y2,’b-',c,y3,'g—','linewidth’,1。2);grid onaxis([0,12,-15,15]);title('l=0 时图解法确定 LP 模的 ha’);text(0。5,3。5,’V=2’);text(3,5,'V=5’);text(4,8,’V=8');xlabel('ha’);ylabel(' Y');set(h,'LineSmoothing’,'on’);