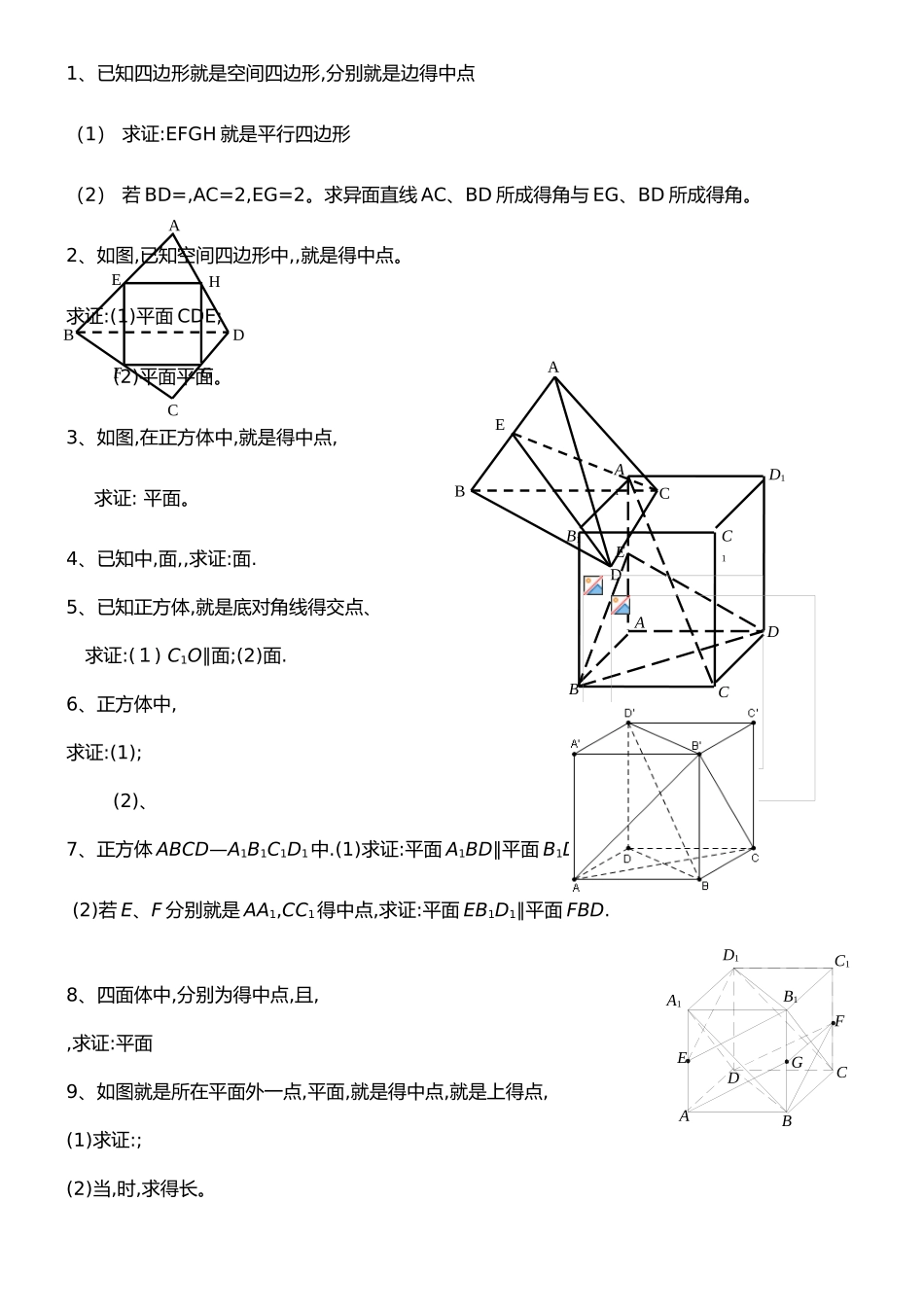
1、已知四边形就是空间四边形,分别就是边得中点(1) 求证:EFGH 就是平行四边形(2) 若 BD=,AC=2,EG=2。求异面直线 AC、BD 所成得角与 EG、BD 所成得角。2、如图,已知空间四边形中,,就是得中点。求证:(1)平面 CDE;(2)平面平面。 3、如图,在正方体中,就是得中点,求证: 平面。4、已知中,面,,求证:面.5、已知正方体,就是底对角线得交点、求证:(1) C1O∥面;(2)面. 6、正方体中,求证:(1);(2)、7、正方体 ABCD—A1B1C1D1中.(1)求证:平面 A1BD∥平面 B1D1C; (2)若 E、F 分别就是 AA1,CC1得中点,求证:平面 EB1D1∥平面 FBD.8、四面体中,分别为得中点,且,,求证:平面 9、如图就是所在平面外一点,平面,就是得中点,就是上得点,(1)求证:;(2)当,时,求得长。A1ED1C1B1DCBAAHGFEDCBAEDBCA1AB1BC1CD1DGEF10、如图,在正方体中,、、分别就是、、得中点、求证:平面∥平面、11、如图,在正方体中,就是得中点、(1)求证:平面;(2)求证:平面平面、12、已知就是矩形,平面,,,为得中点.(1)求证:平面;(2)求直线与平面所成得角.13、如图,在四棱锥中,底面就是且边长为得菱形,侧面就是等边三角形,且平面垂直于底面.(1)若为得中点,求证:平面;(2)求证:;(3)求二面角得大小.14、如图2,在三棱锥A-BCD 中,BC=AC,AD=BD,作 BE⊥CD,E为垂足,作 AH⊥BE 于H.求证:AH⊥平面BCD.1、 证明:在中, 分别就是得中点∴同理,∴∴四边形就是平行四边形。(2) 90° 30 °考点:证平行(利用三角形中位线),异面直线所成得角2、 证明:(1)同理,又 ∴平面(2)由(1)有平面又 平面, ∴平面平面考点:线面垂直,面面垂直得判定3、 证明:连接交于,连接, 为得中点,为得中点∴为三角形得中位线 ∴又在平面内,在平面外∴平面。 考点:线面平行得判定4、 证明:° 又面 面 又面 考点:线面垂直得判定5、 证明:(1)连结,设,连结 就是正方体 就是平行四边形∴A1C1∥AC 且 又分别就是得中点,∴O1C1∥AO 且就是平行四边形 面,面 ∴C1O∥面 (2)面 又, 同理可证, 又面 考点:线面平行得判定(利用平行四边形),线面垂直得判定考点:线面垂直得判定7、 证明:(1)由 B1B∥DD1,得四边形 BB1D1D 就是平行四边形,∴B1D1∥BD,又 BD 平面 B1D1C,B1D1平面 B1D1C,∴BD∥平面 B1D1C.同理 A1D∥平面 B1D1C.而 A1D∩BD=D,∴平面 A1BD∥平面 B1CD. (2)由 BD∥B1D1,得 BD∥平面 EB1D1.取 BB1中点 G,∴AE∥B1G.从而得 B1E∥AG,同理 GF∥AD.∴AG∥DF.∴B1E...