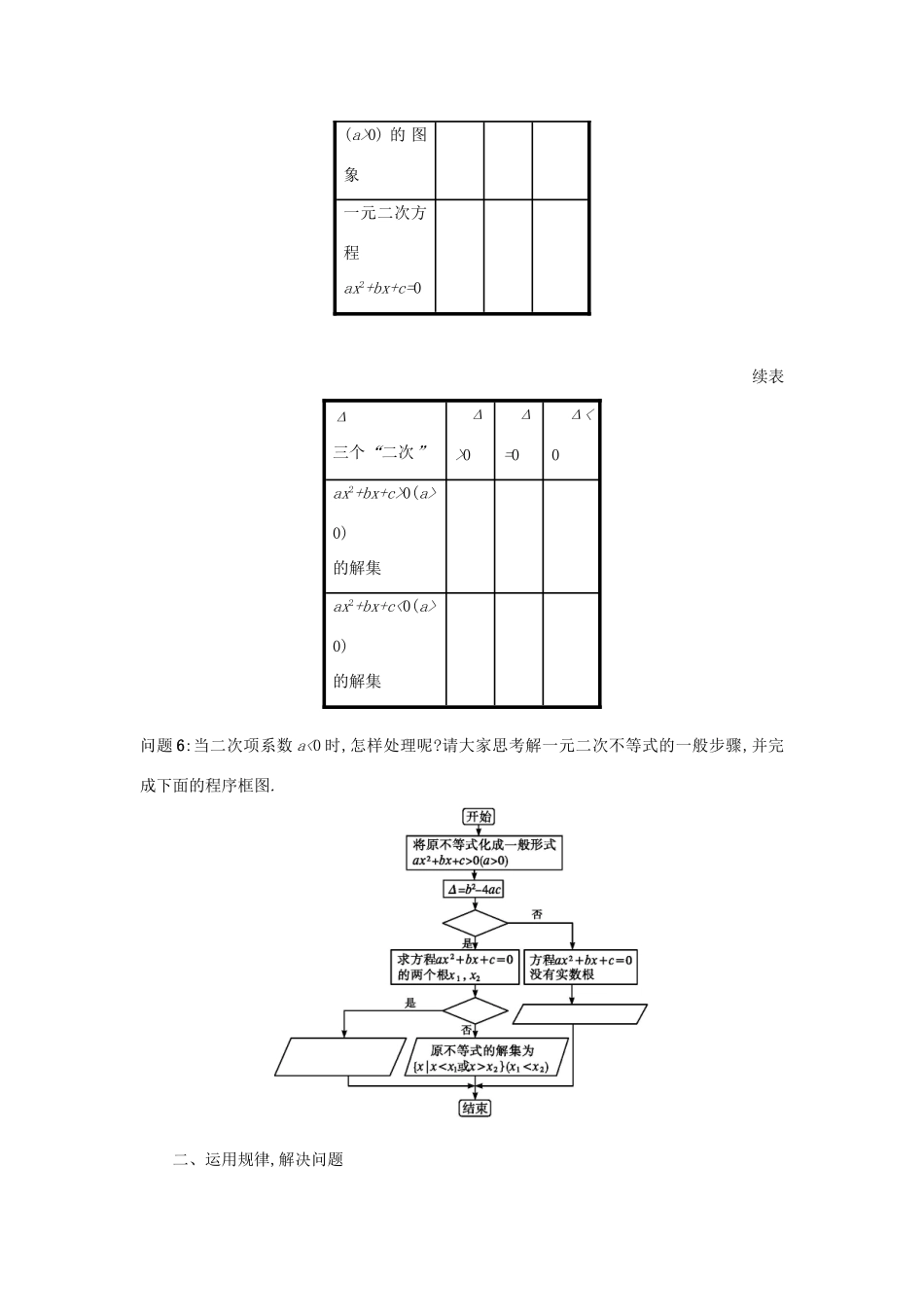
第三章 不等式3.2 一元二次不等式及其解法3.2 一元二次不等式及其解法(第 1 课时)学习目标1.理解一元二次方程、一元二次不等式与二次函数的关系.2.掌握图象法解一元二次不等式的方法.合作学习一、设计问题,创设情境问题 1:观察不等式 x2-4x<0 和-x2+x+2>0,它们有什么共同特征?怎样给这样的不等式命名?它的一般形式是什么?问题 2:请尝试求解不等式 x2-4x<0.问题 3:两种方法分别体现了什么样的数学思想?哪种方法更简洁、直观?请同学们用这种方法求不等式-x2+x+2>0 的解集.问题 4:用数形结合的方法求解一元二次不等式的解集,主要关注相应二次函数图象的什么特征?问 题 5: 上 面 的 方 法 可 以 推 广 到 求 一 般 的 一 元 二 次 不 等 式 ax2+bx+c>0 或ax2+bx+c<0(a>0)解集吗?相应的二次函数图象与 x 轴的交点情形确定吗?由谁决定?怎么处理?(分类讨论)请大家探究.根据探究的情形,完成下表:Δ三 个 “ 二次” Δ>0 Δ=0 Δ<0二次函数y=ax2+bx+c(a>0) 的 图象一元二次方程ax2+bx+c=0续表Δ三个“二次” Δ>0 Δ=0 Δ<0ax2+bx+c>0(a>0)的解集ax2+bx+c<0(a>0)的解集问题 6:当二次项系数 a<0 时,怎样处理呢?请大家思考解一元二次不等式的一般步骤,并完成下面的程序框图.二、运用规律,解决问题【例题】解下列不等式:(1)4x2-4x+1>0;(2)-x2+2x-3>0.三、变式训练,深化提高变式训练 1:解下列不等式:(1)-x2+2x+8≥0;(2)x2-6x+9≤0.变式训练 2:请同学们自己编两道解一元二次不等式的题目,并由同位给出解答,交流解答结果.四、反思小结,观点提炼问题 7:本节课我们主要用什么思想方法推导了一元二次不等式的解法?这种思想对一般的不等式 f(x)>0 可以求解吗?具体步骤是什么?类似的你能用这种方法求不等式 f(x)>k的解集吗?参考答案一、设计问题,创设情境问 题 1: 只 含 有 一 个 未 知 数 , 并 且 未 知 数 的 最 高 次 数 是 2; 一 元 二 次 不 等 式 ;ax2+bx+c>0(<0)(a≠0).问题 2:(数形结合)设 f(x)=x2-4x,画出其图象.容易知道方程 x2-4x=0 的根 x1=0,x2=4,就是函数 f(x)=x2-4x 的零点,也就是函数f(x)=x2-4x 的图象与 x 轴交点的横坐标.而不等式 x2-4x<0 的解集,即 f(x)<0 的解集,也就是函数 f(x)=x2-4x 图象在 x 轴下方的部分对应的横坐标的取值集合为{x|0