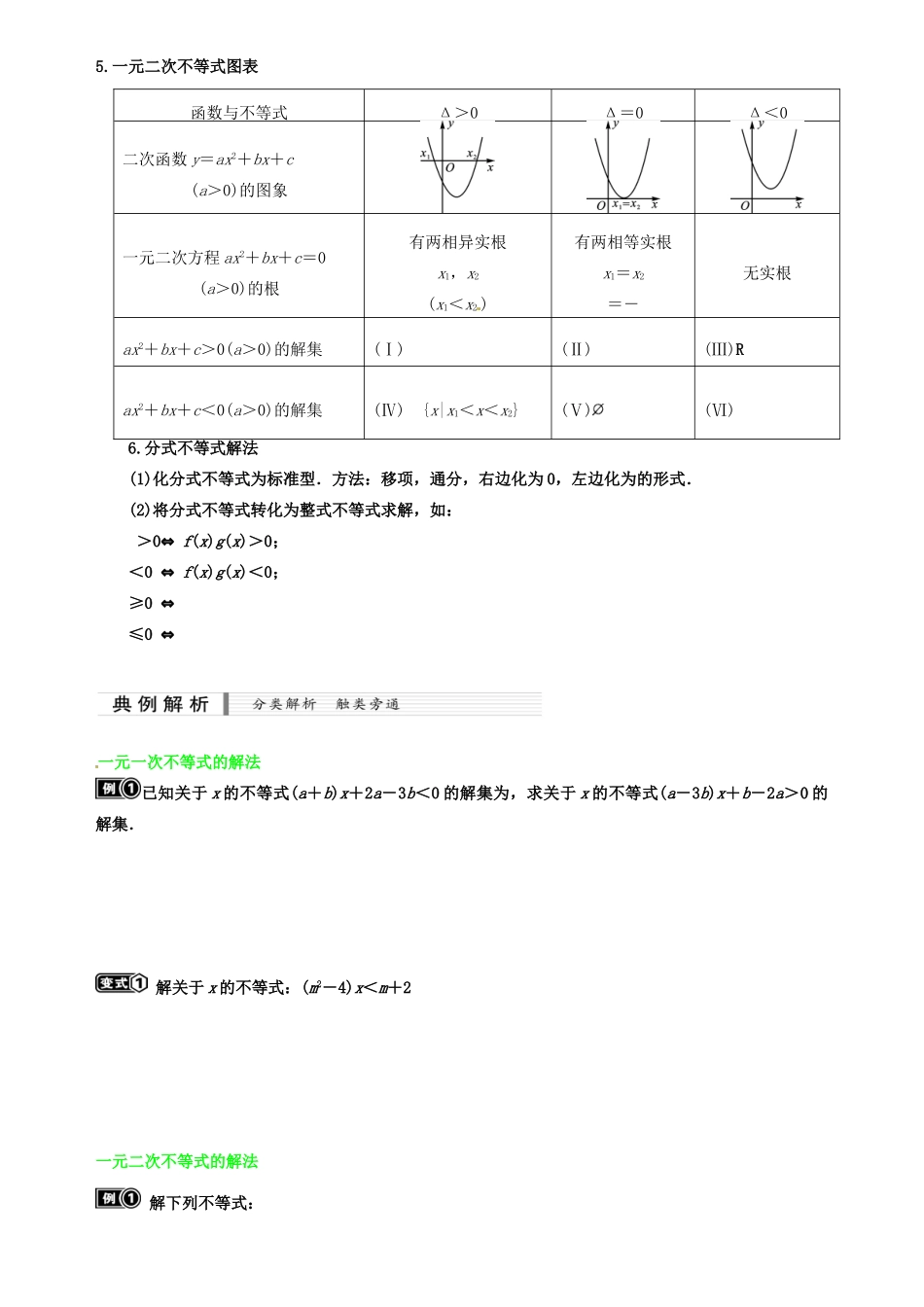
一元二次不等式及其解法1.会从实际问题的情境中抽象出一元二次不等式模型.2.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.3.会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.一元二次不等式的解法是高考必考内容之一,常与函数、数列、平面向量、解析几何、导数等综合起来命题.小题易出现考查“三个二次”关系的题目,多与函数图象及性质、数列、导数等综合考查;解答题中易出现需要分类与整合的含参数的一元二次不等式的综合题,着重考查分类与整 合思想.1.解不等式的有关理论(1)若两个不等式的解集相同,则称它们是 ;(2)一个不等式变形为另一个不等式时,若两个不等式是同解不等式,这种变形称为不等式的 ;(3)解不等式变形时应进行同解变形;解不等式的结果,一般用集合表示.2.一元一次不等式解法任何一个一元一次不等式经过不等式的同解变形后,都可以化为 ax>b(a≠0)的形式.当 a>0 时,解集为 ;当 a<0 时,解集为 .若关于 x 的不等式 ax>b 的解集是 R,则实数 a,b 满足的条件是 .3.一元二次不等式及其解法(1)我们把只含有一个未知数,并且未知数的最高次数是 2 的不等式,称为__________不等式.(2)使某个一元二次不等式成立的 x 的值叫做这个一元二次不等式的解,一元二次不等式所有的解组成的集合叫做一元二次不等式的________.(3)若一元二次不等式经过同解变形后,化为一元二次不等式 ax2+bx+c>0(或 ax2+bx+c<0)(其中 a>0)的形式,其对应的方程 ax2+bx+c=0 有两个不等实根 x1,x2,且 x1<x2(此时 Δ=b2-4ac>0),则可根据“大于号取 ,小于号取 ”求解集.4.一元二次不等式的解法(1)将不等式的右边化为零,左边化为二次项系数大于零的不等式 ax2+bx+c>0(a>0).(2)计算相应的判别式.(3)当 Δ≥0 时,求出相应的一元二次方程的根.(4)利用二次函数的图象与 x 轴的交点确定一元二次不等式的解集5.一元二次不等式图表6.分式不等式解法(1)化分式不等式为标准型.方法:移项,通分,右边化为 0,左边化为的形式.(2)将分式不等式转化为整式不等式求解,如: >0⇔ f(x)g(x)>0;<0 ⇔ f(x)g(x)<0;≥0 ⇔ ≤0 ⇔ 一元一次不等式的解法已知关于 x 的不等式(a+b)x+2a-3b<0 的解集为,求关于 x 的不等式(a-3b)x+b-2a>0 的解集. 解关于 x 的不等式:(m2-4)x<m+2一元二次不等式的解法 解...