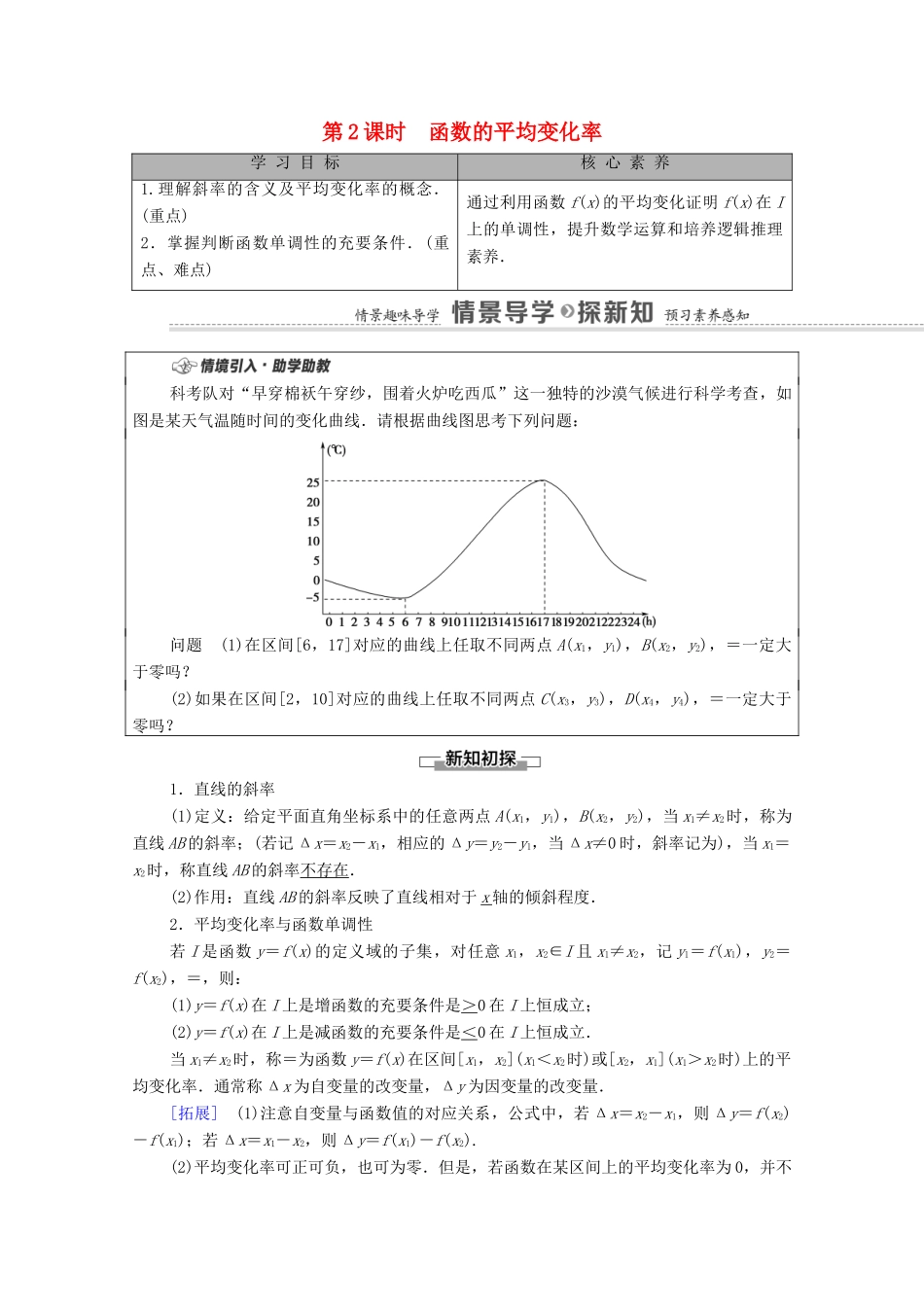
第 2 课时 函数的平均变化率学 习 目 标核 心 素 养1.理解斜率的含义及平均变化率的概念.(重点)2.掌握判断函数单调性的充要条件.(重点、难点)通过利用函数 f(x)的平均变化证明 f(x)在 I上的单调性,提升数学运算和培养逻辑推理素养.科考队对“早穿棉袄午穿纱,围着火炉吃西瓜”这一独特的沙漠气候进行科学考查,如图是某天气温随时间的变化曲线.请根据曲线图思考下列问题:问题 (1)在区间[6,17]对应的曲线上任取不同两点 A(x1,y1),B(x2,y2),=一定大于零吗?(2)如果在区间[2,10]对应的曲线上任取不同两点 C(x3,y3),D(x4,y4),=一定大于零吗?1.直线的斜率(1)定义:给定平面直角坐标系中的任意两点 A(x1,y1),B(x2,y2),当 x1≠x2时,称为直线 AB 的斜率;(若记 Δx=x2-x1,相应的 Δy=y2-y1,当 Δx≠0 时,斜率记为),当 x1=x2时,称直线 AB 的斜率不存在.(2)作用:直线 AB 的斜率反映了直线相对于 x 轴的倾斜程度.2.平均变化率与函数单调性若 I 是函数 y=f(x)的定义域的子集,对任意 x1,x2∈I 且 x1≠x2,记 y1=f(x1),y2=f(x2),=,则:(1)y=f(x)在 I 上是增函数的充要条件是>0 在 I 上恒成立;(2)y=f(x)在 I 上是减函数的充要条件是<0 在 I 上恒成立.当 x1≠x2时,称=为函数 y=f(x)在区间[x1,x2](x1<x2时)或[x2,x1](x1>x2时)上的平均变化率.通常称 Δx 为自变量的改变量,Δy 为因变量的改变量.[拓展] (1)注意自变量与函数值的对应关系,公式中,若 Δx=x2-x1,则 Δy=f(x2)-f(x1);若 Δx=x1-x2,则 Δy=f(x1)-f(x2).(2)平均变化率可正可负,也可为零.但是,若函数在某区间上的平均变化率为 0,并不能说明该函数在此区间上的函数值都相等.比如,f(x)=x2在区间[-2,2]上的平均变化率为 0,但 f(x)=x2在[-2,2]上的图像先下降后上升,值域是[0,4].(3)平均变化率的几何意义是函数 y=f(x)图像上的两点 A(x1,f(x1)),B(x2,f(x2))连线所在直线的斜率.(4)平均变化率是曲线陡峭程度的“数量化”,曲线陡峭程度是平均变化率的“视觉化”.利用平均变化率可以刻画变量平均变化的趋势和快慢程度,但效果是“粗糙不精确的”.只有当 Δx=x2-x1无限变小时,这种量化才由“粗糙”逼近“精确”.3.平均变化率的物理意义(1)把位移 s 看成时间 t 的函数 s=s(t),则平均变化率的物理意义是物体在时间段[t1,t2]上的平...