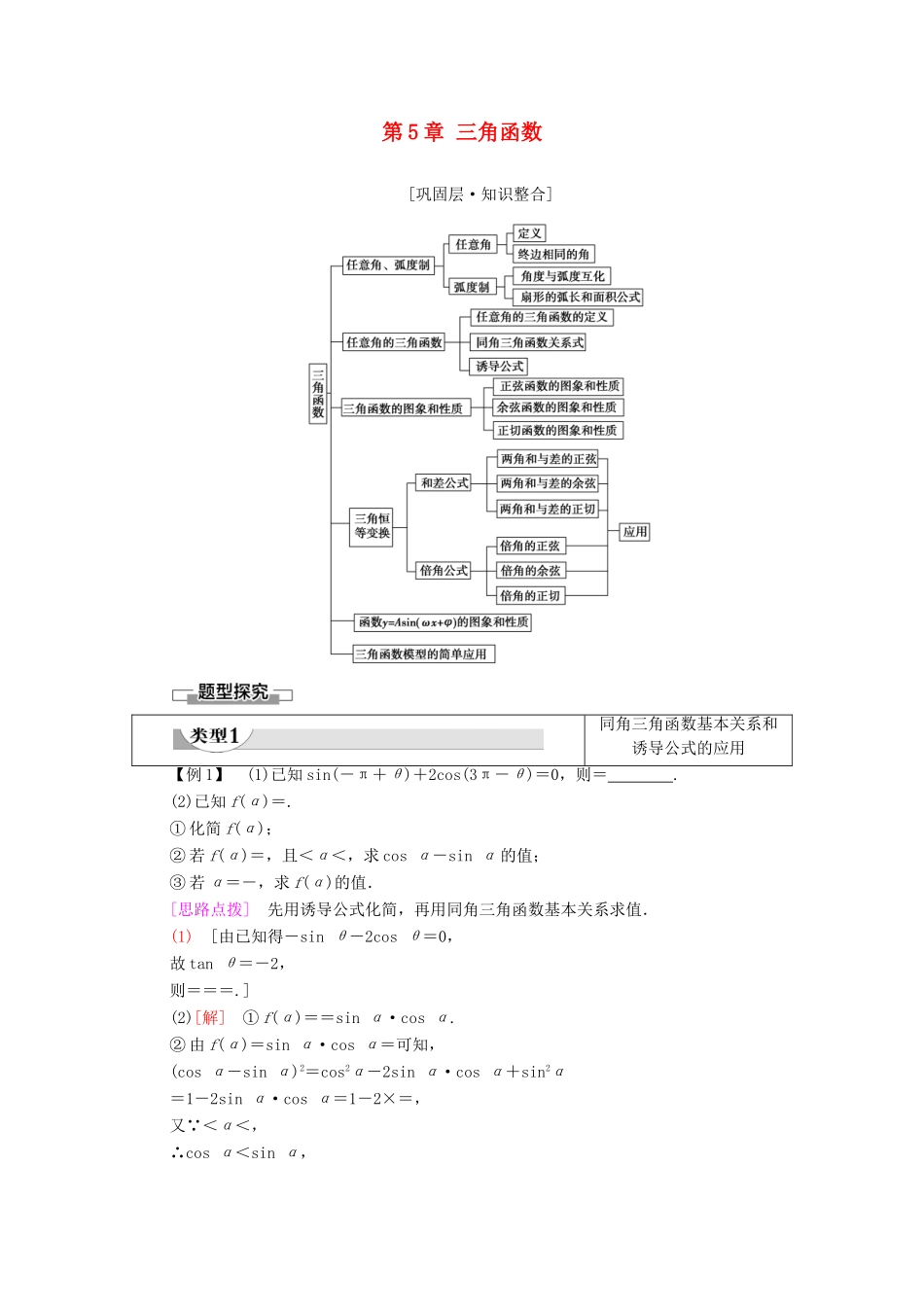
第 5 章 三角函数[巩固层·知识整合]同角三角函数基本关系和诱导公式的应用【例 1】 (1)已知 sin(-π+θ)+2cos(3π-θ)=0,则= .(2)已知 f(α)=.① 化简 f(α);② 若 f(α)=,且<α<,求 cos α-sin α 的值;③ 若 α=-,求 f(α)的值.[思路点拨] 先用诱导公式化简,再用同角三角函数基本关系求值.(1) [由已知得-sin θ-2cos θ=0,故 tan θ=-2,则===.](2)[解] ① f(α)==sin α·cos α.② 由 f(α)=sin α·cos α=可知,(cos α-sin α)2=cos2α-2sin α·cos α+sin2α=1-2sin α·cos α=1-2×=,又 <α<,∴cos α<sin α,即 cos α-sin α<0,∴cos α-sin α=-.③ α=-π=-6×2π+,∴f=cos·sin=cos·sin=cos·sin=×=.1.将本例(2)中“”改为“-”,“<α<”改为“-<α<0”,求 cos α+sin α.[解] 因为-<α<0,所以 cos α>0,sin α<0 且|cos α|>|sin α|,所以 cos α+sin α>0,又(cos α+sin α)2=1+2sin αcos α=1+2×=,所以 cos α+sin α=.2.将本例(2)中的用 tan α 表示.[解] ===.1.牢记两个基本关系式 sin2α+cos2α=1 及=tan α,并能应用两个关系式进行三角函数的求值、化简、证明.在应用中,要注意掌握解题的技巧.比如:已知 sin α±cos α的值,可求 cos αsin α.注意应用(cos α±sin α)2=1±2sin αcos α.2.诱导公式可概括为 k·±α(k∈Z)的各三角函数值的化简公式.记忆规律是:奇变偶不变,符号看象限.三角函数的图象变换问题【例 2】 (1)已知曲线 C1:y=cos x,C2:y=sin,则下面结论正确的是( )A.把 C1上各点的横坐标伸长到原来的 2 倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线 C2B.把 C1上各点的横坐标伸长到原来的 2 倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线 C2C.把 C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线 C2D.把 C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线 C2(2)将函数 y=sin(2x+φ)的图象沿 x 轴向左平移个单位长度后,得到一个偶函数的图象,则 φ 的一个可能取值为( )A. B.C.0 D.-(1)D (2)B [(1)因为 y=sin=cos=cos,...