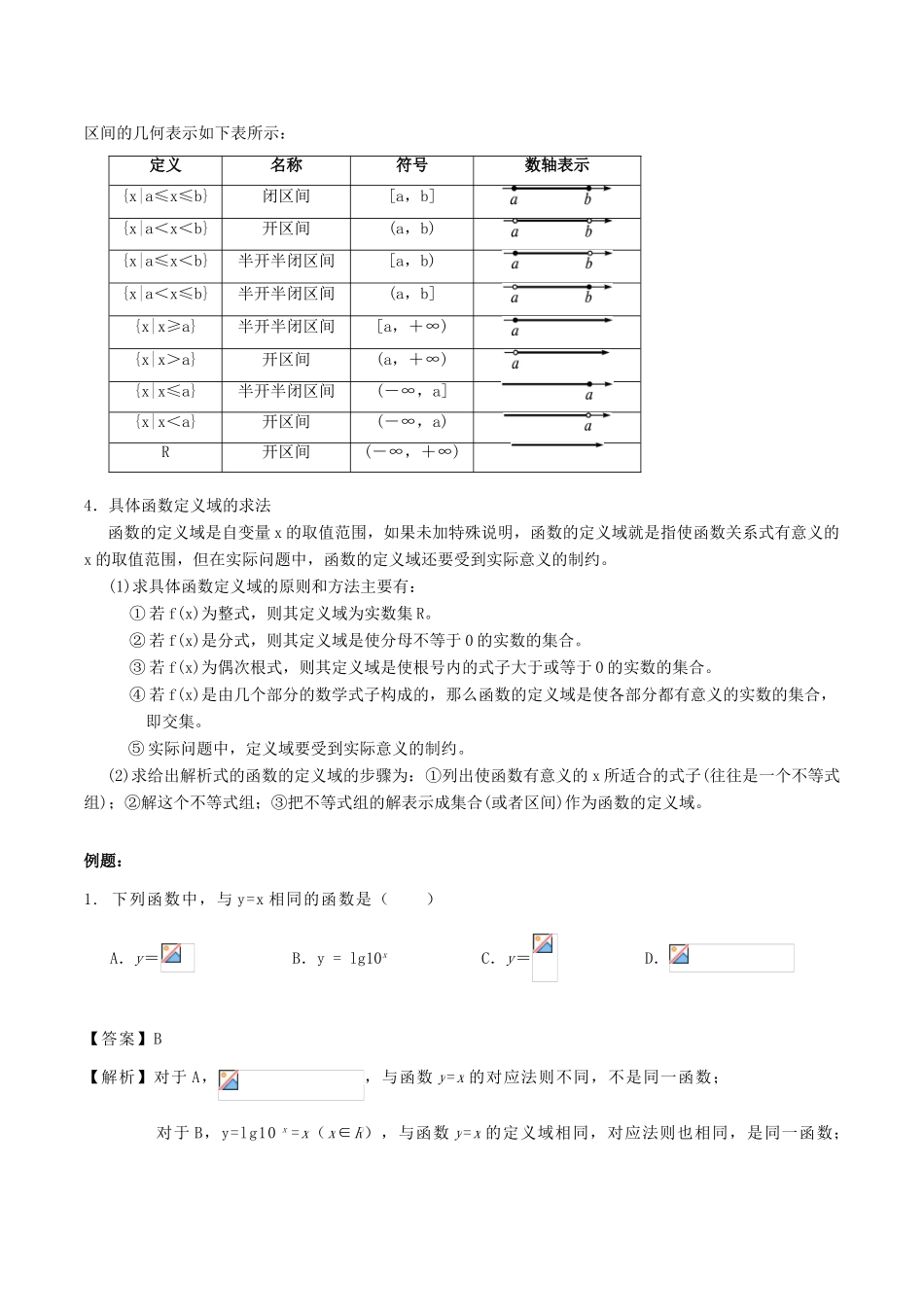
1.2 函数及其表示自主复习考点清单:函数的概念与函数的定义域;函数的表示;分段函数及映射。考点详情:重点一:函数的概念1.函数的概念设是非空数集,如果按照某种对应关系,使集合中任意一个数,在集合中存在唯一确定 的数与之对应,则称为从集合到集合的一个函数,记作。函数的定义域、值域:在函数中,叫自变量,的取值范围叫函数的定义域,与的值对应的值叫函数值,函数值的集合叫函数的值域,显然值域是的子集。2.函数的三要素:定义域、值域、对应法则3.区间:区间是数学中表示“连续”的数集的一种形式。设 a,b 是两个实数,而且 a < b 。我们规定:(1)满足不等式 a≤x≤b 的实数 x 的集合叫做闭区间,表示为[a , b] ;(2)满足不等式 a<x<b 的实数 x 的集合叫做开区间,表示为(a , b) ;(3)满足不等式 a≤x<b 或 a<x≤b 的实数 x 的集合叫做半开半闭区间,分别表示为[a , b) ,(a , b] 。这里的实数 a 与 b 都叫做相应区间的端点.其中 a 叫做左端点,b 叫做右端点。实数集 R 可以用区间表示为(-∞,+∞),“∞”读作“无穷大”,“-∞”读作“负无穷大”,“+∞”读作“正无穷大”。我们可以把满足 x≥a,x>a,x≤b,x<b 的实数 x 的集合分别表示为[a,+∞),(a,+∞),(-∞,b],(-∞,b)。区间的几何表示如下表所示:定义名称符号数轴表示{x|a≤x≤b}闭区间[a,b]{x|a<x<b}开区间(a,b){x|a≤x<b}半开半闭区间[a,b){x|a<x≤b}半开半闭区间(a,b]{x|x≥a}半开半闭区间[a,+∞){x|x>a}开区间(a,+∞){x|x≤a}半开半闭区间(-∞,a]{x|x<a}开区间(-∞,a)R开区间(-∞,+∞)4.具体函数定义域的求法函数的定义域是自变量 x 的取值范围,如果未加特殊说明,函数的定义域就是指使函数关系式有意义的x 的取值范围,但在实际问题中,函数的定义域还要受到实际意义的制约。(1)求具体函数定义域的原则和方法主要有:① 若 f(x)为整式,则其定义域为实数集 R。② 若 f(x)是分式,则其定义域是使分母不等于 0 的实数的集合。③ 若 f(x)为偶次根式,则其定义域是使根号内的式子大于或等于 0 的实数的集合。④ 若 f(x)是由几个部分的数学式子构成的,那么函数的定义域是使各部分都有意义的实数的集合,即交集。⑤ 实际问题中,定义域要受到实际意义的制约。(2)求给出解析式的函数的定义域的步骤为:①列出使函数有意义的 x 所适合的式子(往往...