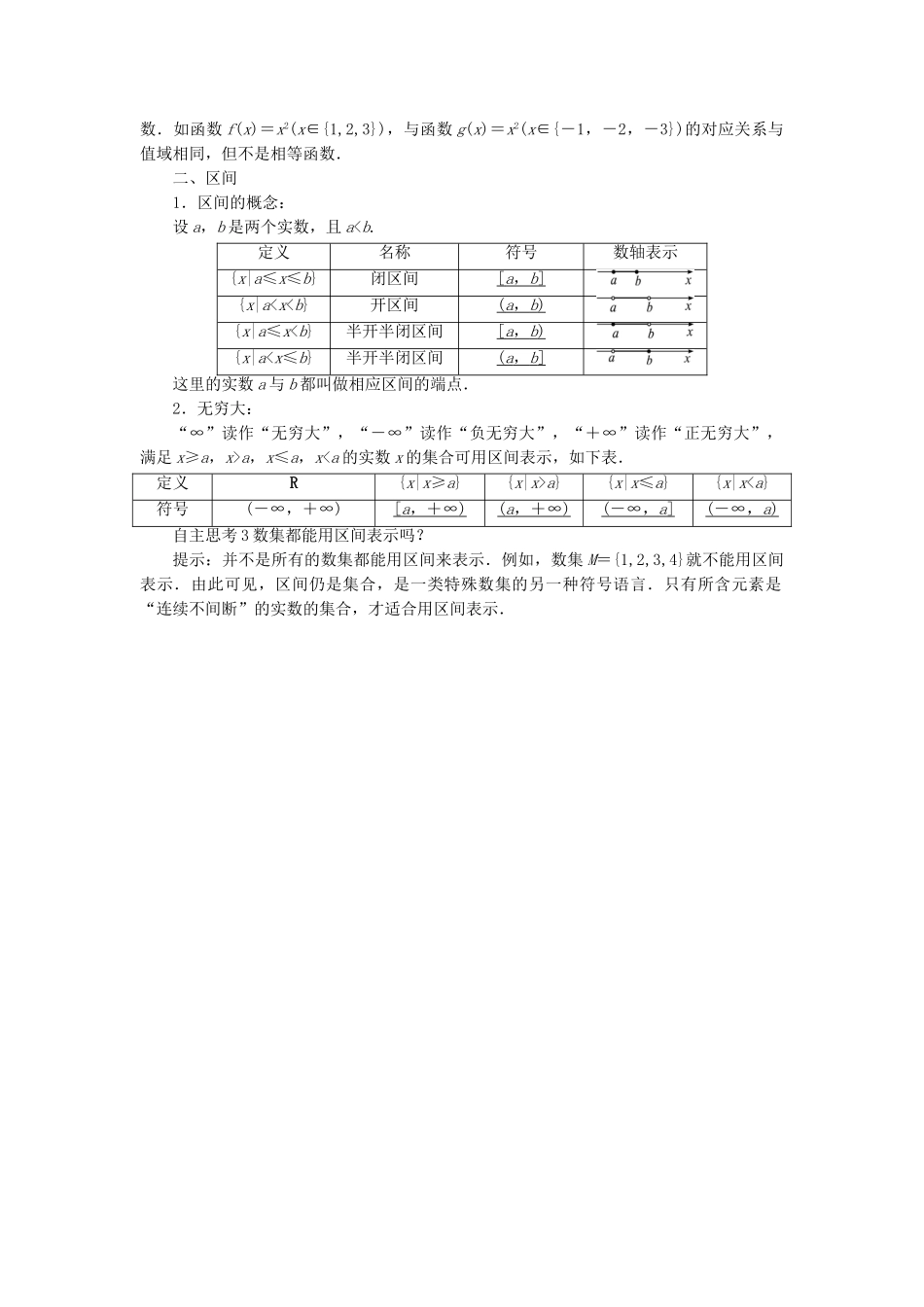
1.2 函数及其表示预习导航课程目标学习脉络1.能够用集合与对应的语言给出函数的定义;知道构成函数的要素,清楚函数的定义中“任意一个数 x ”和“唯一确定的数 f(x)”的含义;明确符号“f(x)”表示的意义.2.会判断两个函数是否相等;会求简单函数的函数值和定义域.一、函数名师点拨 1.“A,B 是非空的数集”,一方面强调了 A,B 只能是数集,即 A,B 中的元素只能是实数;另一方面指出了定义域、值域都不能是空集,也就是说定义域为空集的函数是不存在的.2.函数定义中强调“三性”:任意性、存在性、唯一性,即对于非空数集 A 中的任意一个(任意性)元素 x,在非空数集 B 中都有(存在性)唯一(唯一性)的元素 y 与之对应.这三个性质只要有一个不满足便不能构成函数.3.符号 f(x)与 f(m)既有区别又有联系,当 m 是变量时,函数 f(x)与函数 f(m)相等;当 m 是常数时,f(m)表示当自变量 x=m 时对应的函数值,是一个常量.4.符号 f(x)是函数的记法,是一个整体,它不表示 f 与 x 相乘.自主思考 1 如何判断从集合 A 到集合 B 的一个对应是函数?提示:首先看集合 A,B 是否是非空数集,若不是,则不是函数;若是,然后看集合 A中的每一个元素在集合 B 中是否有元素与之对应,若没有,则不是函数;若有,再看集合B 中是否只有一个元素与之对应,若有多个与之对应,则不是函数;若只有一个与之对应 ,则是函数.自主思考 2 若两个函数的对应关系相同,值域也相同,那么这两个函数是相等函数吗?提示:不一定.若它们的定义域相同,则这两个函数为相等函数,否则,不是相等函数.如函数 f(x)=x2(x∈{1,2,3}),与函数 g(x)=x2(x∈{-1,-2,-3})的对应关系与值域相同,但不是相等函数.二、区间1.区间的概念:设 a,b 是两个实数,且 a
a,x≤a,xa}{x|x≤a}{x|x