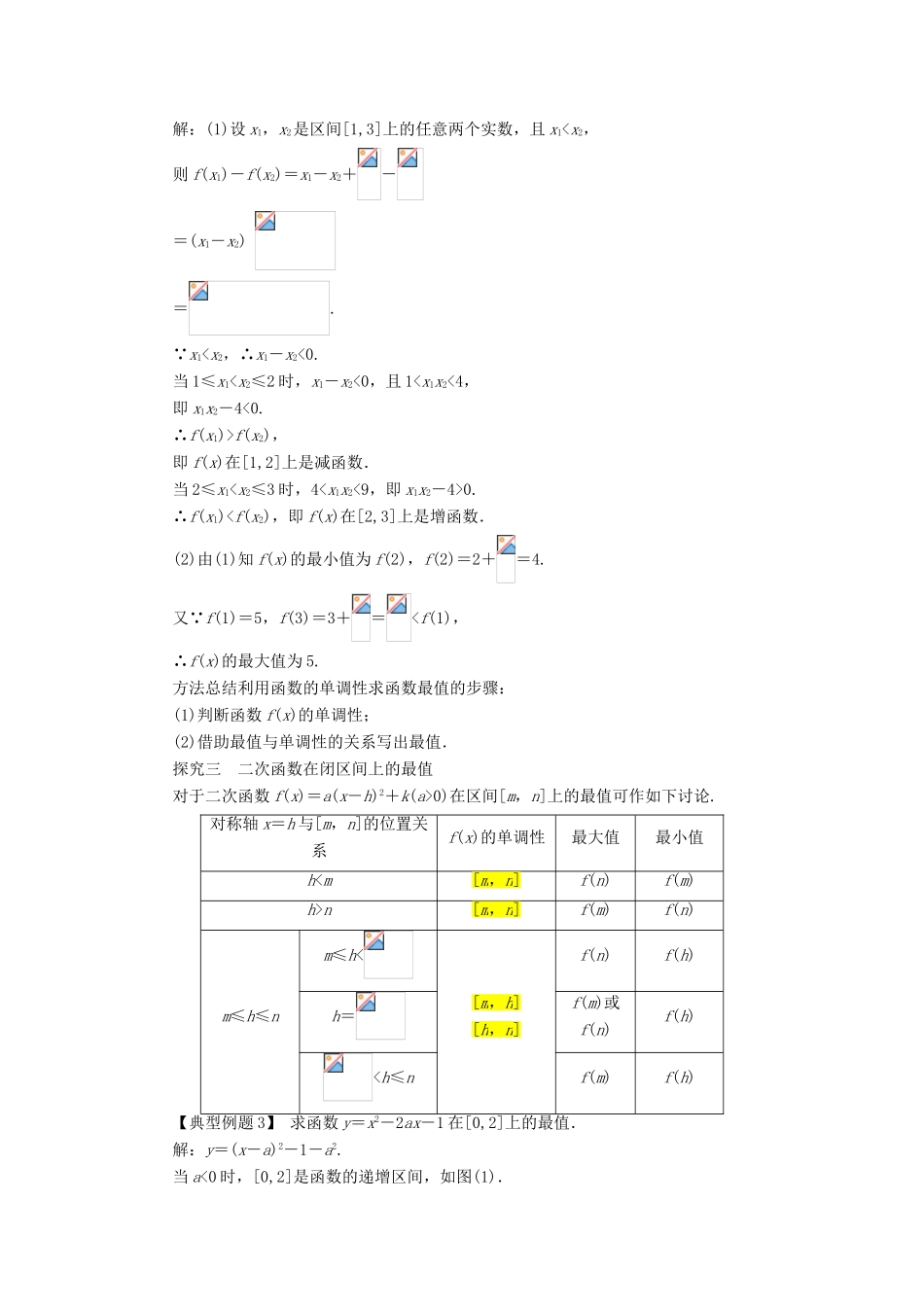
1.3 函数的基本性质课堂探究探究一 利用函数的图象求函数的最值函数的最大值就是函数图象最高点的纵坐标,最小值就是函数图象最低点的纵坐标,因而只要作出函数的图象就可以求出函数的最值,这是求函数最值的常用方法之一.【典型例题 1】 已知函数 f(x)=|x+1|+|x-1|.(1)画出 f(x)的图象;(2)根据图象写出 f(x)的最小值.思路分析:(1)讨论 x 与±1 的大小,化函数 f(x)为分段函数形式;(2)函数图象的最低点的纵坐标是 f(x)的最小值.解:(1)f(x)=|x+1|+|x-1|=其图象如图所示.(2)由图象,得函数 f(x)的最小值是 2.方法小结用图象法求函数 y=f(x)的最值的步骤:(1)画出函数 y=f(x)的图象;(2)依据函数最值的几何意义,借助图象写出最值.探究二 利用函数的单调性求最值1.函数的单调性是其定义域的子集上的性质,是“局部”性质,而函数的最值是整个定义域上的性质,是“整体”性质.2.若函数 f(x)在[a,b]上是增(减)函数,则 f(x)在[a,b]上的最小(大)值是 f(a),最大(小)值是 f(b).3.若函数 f(x)在[a,b]上是增(减)函数,在[b,c]上是减(增)函数,则 f(x)在[a,c]上的最大(小)值是 f(b),最小(大)值是 f(a)与 f(c)中较小(大)的一个.函数 f(x)在闭区间[a,b]上的图象是一条连续不断的曲线,则函数 f(x)在[a,b]上一定有最值.【典型例题 2】 已知函数 f(x)=x+,x∈[1,3].(1)判断 f(x)在[1,2]和[2,3]上的单调性;(2)根据 f(x)的单调性写出 f(x)的最值.分析:(1)证明单调性的流程:取值→作差→变形→判断符号→结论;(2)借助最值与单调性的关系,写出最值.解:(1)设 x1,x2是区间[1,3]上的任意两个实数,且 x1f(x2),即 f(x)在[1,2]上是减函数.当 2≤x10.∴f(x1)0)在区间[m,n]上的最值可作如下讨论.对称轴 x=h 与[m,n]的位置关系f(x)的单调性最大值最小值h